Advertisements
Advertisements
प्रश्न
Using the formula, tan 2A =`(2 tan A )/(1- tan^2 A)` find the value of tan 600, it being given that tan 300 = `1/sqrt(3)`.
उत्तर
A = 300
⇒ 2A = 2 × 300 = 600
By substituting the value of the given T-ratio, we get:
tan 2A = `(2 tan A )/(1- tan^2 A)`
`⇒ tan 60^0 = (2 tan 30^0)/(1- tan^2 30^0) = (2xx (1/sqrt(3)))/(1-(1/sqrt(3))^2 ` =` ((2/sqrt(3)))/(1-1/3) = ((2/sqrt(3)))/(2/3) = (2/sqrt(3))= 3/2 = sqrt(3) `
∴tan` 60^0 = sqrt(3)`.
APPEARS IN
संबंधित प्रश्न
f θ = 30°, verify that cos 3θ = 4 cos3 θ − 3 cos θ
If A = 450 , verify that:
(ii) cos 2A = 2 cos2 A – 1 = 1 – 2 sin2 A
If A = 300 , verify that:
(ii) cos 2A = `(1- tan^2A)/(1+tan^2A)`
Given: cos A = 0.6; find all other trigonometrical ratios for angle A.
In a right-angled triangle, it is given that A is an acute angle and tan A = `(5) /(12)`.
find the value of :
(i) cos A
(ii) sin A
(iii) ` (cosA+sinA)/(cosA– sin A)`
Given : 17 cos θ = 15;
Find the value of: tan θ + 2 secθ .
In the given figure, PQR is a triangle, in which QS ⊥ PR, QS = 3 cm, PS = 4 cm and QR = 12 cm, find the value of: sin P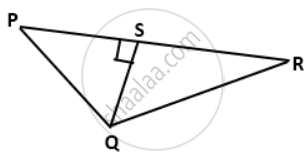
In the given figure, AD is the median on BC from A. If AD = 8 cm and BC = 12 cm, find the value of tan x. cot y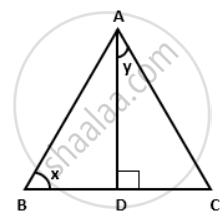
In the given figure, ΔABC is right angled at B.AD divides BC in the ratio 1 : 2. Find
(i) `("tan"∠"BAC")/("tan"∠"BAD")` (ii) `("cot"∠"BAC")/("cot"∠"BAD")`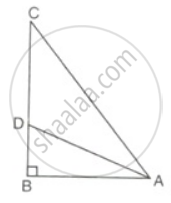
Statement A (Assertion): For 0 < θ ≤ 90°, cosec θ – cot θ and cosec θ + cot θ are reciprocal of each other.
Statement R (Reason): cosec2 θ – cot2 θ = 1
