Advertisements
Advertisements
प्रश्न
If A = 300 , verify that:
(ii) cos 2A = `(1- tan^2A)/(1+tan^2A)`
उत्तर
A = 300
⇒ 2A = 2 × 300 = 600
(ii) cos 2A = cos `60^0 = 1/2`
`(1- tan62 A)/(1+ tan^2 A) = (1-tan^2 30^0)/(1+ tan^2 30^0)= (1-(1/sqrt(3))^2)/(1+(1/sqrt(3))^2` = `(1-(1/3))/(1+(1/3)) = ((2/3))/(4/3) = (2/3)xx3/4=1/2`
∴ cos 2A = `(1-tan^2A)/(1+ tan^2A)`
APPEARS IN
संबंधित प्रश्न
If sec 2A = cosec (A – 42°) where 2A is an acute angle. Find the value of A.
If sin θ = `3/4` show that `sqrt((cosec^2theta - cot^2theta)/(sec^2theta-1)) =sqrt(7)/3`
Evaluate:
`(sin^2 30^0 + 4 cot^2 45^0-sec^2 60^0)(cosec^2 45^0 sec^2 30^0)`
Using the formula, sin A = `sqrt((1-cos 2A)/2) ` find the value of sin 300, it being given that cos 600 = `1/2`
In a right-angled triangle, it is given that A is an acute angle and tan A = `(5) /(12)`.
find the value of :
(i) cos A
(ii) sin A
(iii) ` (cosA+sinA)/(cosA– sin A)`
Using the measurements given in the following figure:
(i) Find the value of sin θ and tan θ.
(ii) Write an expression for AD in terms of θ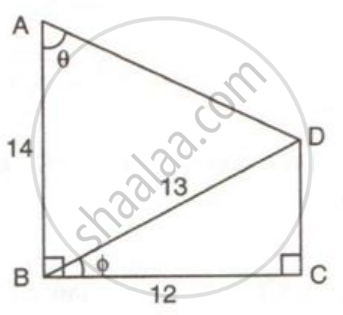
In rectangle ABCD, diagonal BD = 26 cm and cotangent of angle ABD = 1.5. Find the area and the perimeter of the rectangle ABCD.
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
cos A = `(7)/(25)`
If 2 cos θ = `sqrt(3)`, then find all the trigonometric ratios of angle θ
If cos A = `(2x)/(1 + x^2)`, then find the values of sin A and tan A in terms of x
