Advertisements
Advertisements
प्रश्न
If sin θ = ` (a^2 - b^2)/(a^2+b^2)`find all the values of all T-ratios of θ .
उत्तर
We have sin θ = `(a^2 - b^2)/(a^2 + b^2)`
As,
`Cos^2 θ = 1 - sin^2 θ`
`= 1- ((a^2 -b^2)/(a^2 + b^2))^2`
`= 1/1 - ((a^2 - b^2)/(a^2 + b^2))^2`
`= ((a^2 + b^2)^2 -( a^2 - b^2)^2)/(a^2 + b^2)^2`
`= ([(a^2 +b^2)-(a^2-b^2)][(a^2+b^2)+(a^2-b^2)])/((a^2+b^2)^2)`
`= ([(a^2 + b^2-a^2 +b^2][a^2+b^2+a^2-b^2)])/((a^2+b^2)^2)`
`= ([2b^2][2a^2])/((a^2+b^2)^2)`
`= cos^2 θ = (4a^2b^2)/((a^2+b^2)^2)`
`= cosθ= sqrt((4a^2b^2)/(a^2+b^2)^2)`
`⟹ cos θ =(2ab)/((a^2+b^2))`
Also,
tan θ = `sinθ/cosθ`
`= (((a^2-b^2)/(a^2+b^2)))/(((2ab)/(a^2 +b^2))`
`=(a^2-b^2)/(2ab)`
Now ,
cosec θ =` 1/sinθ`
=`1/(((a^2-b^2)/(a^2-b^2)))`
`= (a^2 + b^2)/(2ab)`
Also,
sec θ`= 1/(cosθ)`
= `1/(((2ab)/(a^2+b^2)))`
= `(a^2+b^2)/(2ab)`
And,
cot θ = `1/( tan θ)`
`= 1/(((a^2-b^2)/(2ab)))`
`= (2ab)/(a^2-b^2)`
APPEARS IN
संबंधित प्रश्न
If sin A = `9/41` find all the values of cos A and tan A
Show that:
(i)` (1-sin 60^0)/(cos 60^0)=(tan60^0-1)/(tan60^0+1)`
In the adjoining figure, ΔABC is right-angled at B and ∠A = 300. If BC = 6cm, find (i) AB, (ii) AC.
If sin (A – B) = `1/2` and cos (A + B) = `1/2, 0^0 ≤ (A + B) ≤ 90^0` and A > B, then find A and B.
If sin (A+B) = sin A cos B + cos A sin B and cos (A-B) = cos A cos B + sin A sin B
(i) sin (750)
(ii) cos (150)
sin20° = cos ______°
Given: 4 cot A = 3
find :
(i) sin A
(ii) sec A
(iii) cosec2A - cot2A.
If sin A = cos A, find the value of 2 tan2A - 2 sec2 A + 5.
In the given figure, PQR is a triangle, in which QS ⊥ PR, QS = 3 cm, PS = 4 cm and QR = 12 cm, find the value of: sin P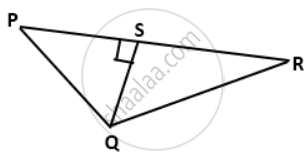
If cos θ : sin θ = 1 : 2, then find the value of `(8costheta - 2sintheta)/(4costheta + 2sintheta`
