Advertisements
Advertisements
प्रश्न
If Sec 4A = cosec (A – 20°) where 4A is an acute angle, find the value of A.
उत्तर
Sec 4A = sec [90 − 𝐴 − 20] [∵ sec(90 − θ) = cosec θ]
Sec 4A = sec (90 – A + 20)
Sec 4A = sec (110 – A)
4A = 110 – A
5A = 110
`A = 110/5 => A = 22`
APPEARS IN
संबंधित प्रश्न
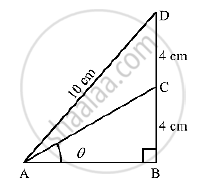
In the adjoining figure, `∠B = 90° , ∠BAC = theta° , BC = CD = 4cm and AD = 10 cm`. find (i) sin theta and (ii) `costheta`
If A and B are acute angles such that tan A =`1/3, tan B = 1/2 and tan (A + B) =` show that `A+B = 45^0`
If sin (A+B) = sin A cos B + cos A sin B and cos (A-B) = cos A cos B + sin A sin B
(i) sin (750)
(ii) cos (150)
From the following figure, find the values of
(i) sin B
(ii) tan C
(iii) sec2 B - tan2B
(iv) sin2C + cos2C
Given: cos A = `( 5 )/ ( 13 )`
Evaluate:
- `(sin "A "–cot "A") / (2 tan "A")`
- `cot "A" + 1/cos"A"`
In rectangle ABCD, diagonal BD = 26 cm and cotangent of angle ABD = 1.5. Find the area and the perimeter of the rectangle ABCD.
If cosec A + sin A = 5`(1)/(5)`, find the value of cosec2A + sin2A.
In ΔABC, ∠A = 90°. If AB = 5 units and AC = 12 units, find: sinB
If sin A = `(7)/(25)`, find the value of : cot2A - cosec2A
If sin θ = `"a"/sqrt("a"^2 + "b"^2)`, then show that b sin θ = a cos θ
