Advertisements
Advertisements
प्रश्न
From the given figure, find the values of tan C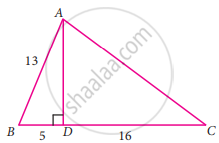
उत्तर
In the right ΔABD,
AD2 = AB2 – BD2
= 132 – 52
= 169 – 25
= 144
AD = `sqrt(144)`
= 12
In the right ΔADC,
AC2 = AD2 + DC2
= 122 + 162
= 144 + 256
= 400
AC = `sqrt(400)`
= 20
tan C = `"opposite side"/"adjacent side" = "AD"/"DC" = 12/16 = 3/4`
APPEARS IN
संबंधित प्रश्न
if `sin theta = 3/5 " evaluate " (cos theta - 1/(tan theta))/(2 cot theta)`
If ∠A and ∠P are acute angles such that tan A = tan P, then show that ∠A = ∠P.
cos 40° = sin ______°
Form the following figure, find the values of:
- cos B
- tan C
- sin2B + cos2B
- sin B. cos C + cos B. sin C

If sin A + cosec A = 2;
Find the value of sin2 A + cosec2 A.
Given q tan A = p, find the value of:
`("p" sin "A" – "q" cos "A")/("p" sin "A" + "q" cos "A")`.
From the given figure, find the values of sec B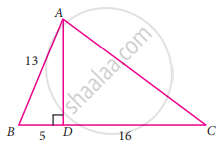
If cos A = `3/5`, then find the value of `(sin"A" - cos"A")/(2tan"A")`
If sin θ = `"a"/sqrt("a"^2 + "b"^2)`, then show that b sin θ = a cos θ
If 3 cot A = 2, then find the value of `(4sin"A" - 3cos"A")/(2sin"A" + 3cos"A")`
