Advertisements
Advertisements
प्रश्न
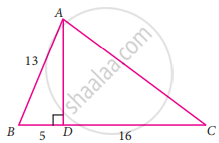
In the given figure, AD is the median on BC from A. If AD = 8 cm and BC = 12 cm, find the value of sin x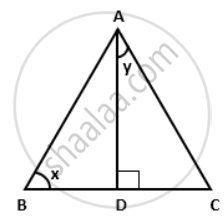
उत्तर
Since AD is median on BC, we have
BD = DC = `(1)/(2) xx "BC" = (1)/(2) xx 12` = 6cm
ΔADB is a right-angled triangle.
∴ AB2
= AD2 + BD2
= 82 + 62
= 64 + 36
= 100
⇒ AB = 10cm
ΔADC is a right-angled triangle.
∴ AC2
= AD2 + DC2
= 82 + 62
= 64 + 36
= 100
⇒ AC = 10cm
sin x
= `"AD"/"AB"`
= `(8)/(10)`
= `(4)/(5)`.
APPEARS IN
संबंधित प्रश्न
If tan θ = `20/21` show that `((1-sin θ + cos θ))/((1+ sin θ +cos θ)) = 3/7`
In ΔABC , ∠C = 90° ∠ABC = θ° BC = 21 units . and AB= 29 units. Show thaT `(cos^2 theta - sin^2 theta)=41/841`
Verify each of the following:
(iii) `2 sin 30^0 cos 30^0`
In the adjoining figure, ΔABC is a right-angled triangle in which ∠B = 900, ∠300 and AC = 20cm. Find (i) BC, (ii) AB.
If sin (A – B) = `1/2` and cos (A + B) = `1/2, 0^0 ≤ (A + B) ≤ 90^0` and A > B, then find A and B.
In the given figure;
BC = 15 cm and sin B = `(4)/(5)`
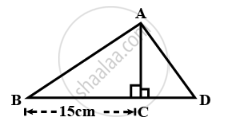
- Calculate the measure of AB and AC.
- Now, if tan ∠ADC = 1; calculate the measures of CD and AD.
Also, show that: tan2B - `1/cos^2 "B" = – 1 .`
In rhombus ABCD, diagonals AC and BD intersect each other at point O.
If cosine of angle CAB is 0.6 and OB = 8 cm, find the lengths of the side and the diagonals of the rhombus.
If cosB = `(1)/(3)` and ∠C = 90°, find sin A, and B and cot A.
If sinA = 0.8, find the other trigonometric ratios for A.
From the given figure, find the values of cot B