Advertisements
Advertisements
प्रश्न
Evaluate the Following
`(sin 30^@ - sin 90^2 + 2 cos 0^@)/(tan 30^@ tan 60^@)`
उत्तर
`(sin 30^@ - sin 90^2 + 2 cos 0^@)/(tan 30^@ tan 60^@)` ...(i)
By trigonometric ratios we have
`sin 30^@ = 1/2, sin 90^@ = 1, cos 0^@ = 1, tan 30^@ = 1/sqrt3 , tan 60^@ = sqrt3`
By substituting above values in (i), we get
`(1/2 1 + 2)/(sqrt3 1/sqrt3) = (3/2 + 1)/1 = 3/2`
APPEARS IN
संबंधित प्रश्न
In ΔABC right angled at B, AB = 24 cm, BC = 7 m. Determine:
sin C, cos C
if `cot theta = 3/4` prove that `sqrt((sec theta - cosec theta)/(sec theta +cosec theta)) = 1/sqrt7`
Evaluate the Following
4(sin4 60° + cos4 30°) − 3(tan2 60° − tan2 45°) + 5 cos2 45°
Evaluate the Following
cosec3 30° cos 60° tan3 45° sin2 90° sec2 45° cot 30°
Evaluate the Following
`(tan^2 60^@ + 4 cos^2 45^@ + 3 sec^2 30^@ + 5 cos^2 90)/(cosec 30^@ + sec 60^@ - cot^2 30^@)`
Evaluate the Following
`sin 30^2/sin 45^@ + tan 45^@/sec 60^@ - sin 60^@/cot 45^@ - cos 30^@/sin 90^@`
Find the value of x in the following :
`2 sin x/2 = 1`
Find the value of x in the following :
`sqrt3 sin x = cos x`
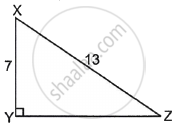
In the given figure, if sin θ = `7/13`, which angle will be θ?
Prove that: cot θ + tan θ = cosec θ·sec θ
Proof: L.H.S. = cot θ + tan θ
= `square/square + square/square` ......`[∵ cot θ = square/square, tan θ = square/square]`
= `(square + square)/(square xx square)` .....`[∵ square + square = 1]`
= `1/(square xx square)`
= `1/square xx 1/square`
= cosec θ·sec θ ......`[∵ "cosec" θ = 1/square, sec θ = 1/square]`
= R.H.S.
∴ L.H.S. = R.H.S.
∴ cot θ + tan θ = cosec·sec θ
