Advertisements
Advertisements
प्रश्न
The angle of elevation of the top of a tower from two points distant s and t from its foot are complementary. Prove that the height of the tower is `sqrt(st)`
उत्तर
Let the height of the tower is h.
And ∠ABC = θ
Given that, BC = s, PC = t
And angle of elevation on both positions are complementary.
i.e., ∠APC = 90° – θ ...[If two angles are complementary to each other, then the sum of both angles is equal to 90°]
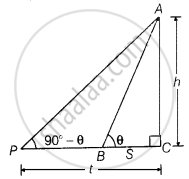
Now in ΔABC,
tan θ = `"AC"/"BC" = "h"/"s"` ...(i)
And in ΔAPC,
tan(90° – θ) = `"AC"/"PC"` ...[∵ tan(90° – θ) = cot θ]
⇒ cot θ = `"h"/"t"`
⇒ `1/tanθ = "h"/"t"` `[∵ cot θ = 1/tan θ]` ...(ii)
On, multiplying equations (i) and (ii), we get
`tan θ * 1/tanθ = "h"/"s" * "h"/"t"`
⇒ `"h"^2/("st")` = 1
⇒ h2 = st
⇒ h = `sqrt("st")`
So, the required height of the tower is `sqrt("st")`.
Hence proved.
APPEARS IN
संबंधित प्रश्न
A passenger, while boarding the plane, slipped form the stairs and got hurt. The pilot took the passenger in the emergency clinic at the airport for treatment. Due to this, the plane got delayed by half an hour. To reach the destination 1500 km away in time, so that the passengers could catch the connecting flight, the speed of the plane was increased by 250 km/hour than the usual speed. Find the usual speed of the plane
What value is depicted in this question?
From a point P on the ground the angle of elevation of the top of a tower is 30° and that of the top of a flag staff fixed on the top of the tower, is 60°. If the length of the flag staff is 5 m, find the height of the tower.
The altitude of the sun at any instant is 60º. Find the height of the vertical pole that will cast a shadow of 30 m.
The heights of two poles are 80 m and 62.5 m. If the line joining their tops makes an angle of 45º with the horizontal, then find the distance between the pole
An observer 1.5m tall is 30 away from a chimney. The angle of elevation of the top of the chimney from his eye is 60 . Find the height of the chimney.
The angles of depression of the top and bottom of a tower as seen from the top of a 60 `sqrt(3)` m high cliff are 45° and 60° respectively. Find the height of the tower.
In the following figure, what are the angles of depression from the observing position O1 and O2of the object at A?
The tops of two poles of heights 20 m and 14 m are connected by a wire. If the wire makes an angle of 30° with the horizontal, then the length of the wire is ____________.
A 1.5 m tall boy is standing at some distance from a 31.5 m tall building. If he walks ’d’ m towards the building the angle of elevation of the top of the building changes from 30° to 60°. Find the length d. (Take `sqrt3 = 1.73`)
The angle of elevation of the top of a tower is 30°. If the height of the tower is doubled, then the angle of elevation of its top will also be doubled.
