Advertisements
Advertisements
प्रश्न
A man standing on the deck of a ship, which is 8 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill.
उत्तर
Let H be the height of hill CE and a man is standing on a ship at the height of 8meter above from the water level.
Let AB = 8, BC = x, AD = BC, AB = DC, DE = h.
∠ACB = 30° and ∠DAE = 60°
We have to find x and H
The corresponding figure is as follows
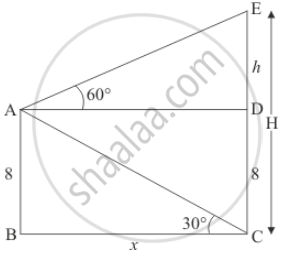
In ΔABC
`=> tan 30 = 8/x`
`=> 1/sqrt3 = 8/x`
`=> x = 8sqrt3`
Again in Δ DAE,
`=> tan 60^@ = h/x`
`=> sqrt3 = h/x`
`=> h = xsqrt3`
`=> h = 24`
Therefore H = h + 8`
`=> H = 24 + 8`
=> H = 32
Hence the required distance is `8sqrt3`m and height is 32 m
APPEARS IN
संबंधित प्रश्न
The shadow of a building is 20 m long when the angle of elevation of the sun is 60º. Find the height of the building
A man on the deck of a ship is 10 m above the water level. He observes that the angle of elevation of the top of a cliff is 45° and the angle of depression of the base is 300. Calculate the distance of the cliff from the ship and the height of the cliff.
An aeroplane flying horizontally 1 km above the ground is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°. Find the speed of the aeroplane in km/hr.
PQ is a post of given height a, and AB is a tower at some distance. If α and β are the angles of elevation of B, the top of the tower, at P and Q respectively. Find the height of the tower and its distance from the post.
The angle of elevation of the top of a chimney form the foot of a tower is 60° and the angle of depression of the foot of the chimney from the top of the tower is 30° . If the height of the tower is 40 meters. Find the height of the chimney.
Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angels of elevation of the top of the poles are 60° and 30° respectively.
Find the height of the poles and the distances of the point from the poles.
The Distance of the point (−3, 4) from the x-axis is
In given Fig., the angle of depression from the observing position D and E of the object at A are ____________.
A portion of a 60 m long tree is broken by a tornado and the top struck up the ground making an angle of 30° with the ground level. The height of the point where the tree is broken is equal to ____________.
A pole 6 m high casts a shadow `2sqrt(3)` m long on the ground, then the Sun’s elevation is ______.
