Advertisements
Advertisements
प्रश्न
From the top of a tree of height 13 m the angle of elevation and depression of the top and bottom of another tree are 45° and 30° respectively. Find the height of the second tree. `(sqrt(3) = 1.732)`
उत्तर
Let the height of the second tree be “h”
ED = (h – 13) m
Let AB = x m
In the right ∆ABC, tan 30° = `"BC"/"AB"`
`1/sqrt(3) = 13/x`
x = `13sqrt(3)` ...(1)
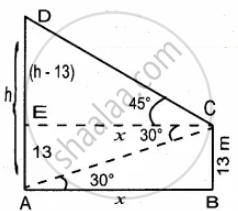
In the right ∆CED, tan 45° = `"DE"/"EC"`
1 = `("h" - 13)/x`
x = h – 13 ...(2)
From (1) and (2) we get
h – 13 = `13sqrt(3)`
⇒ h = `13sqrt(3) + 13`
= 13 × 1.732 + 13
= 22.52 + 13
= 35.52 m
∴ Height of the second tree = 35.52 m
APPEARS IN
संबंधित प्रश्न
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 45°. If the tower is 30 m high, find the height of the building.
An electric pole is 10 m high. A steel wire tied to the top of the pole is affixed at a point on the ground to keep the pole upright. If the wire makes an angle of 45° with the horizontal through the foot of the pole, find the length of the wire.
From the top of a building AB, 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find
1) the horizontal distance between AB and CD
2) the height of the lamp post.
3) the difference between the heights of the building and the lamp post.
While landing at an airport, a pilot made an angle of depression of 20°. Average speed of the plane was 200 km/hr. The plane reached the ground after 54 seconds. Find the height at which the plane was when it started landing. (sin 20° = 0.342)

Radii of the top and the base of a frustum of a cone are 5 cm and 2 cm respectively. Its height is 9 cm. Find its volume. (π = 3.14)
AB is a pole of height 6 m standing at a point B and CD is a ladder inclined at angle of 600 to the horizontal and reaches upto a point D of pole . If AD = 2.54 m , find the length of the ladder.
A building and a statue are in opposite side of a street from each other 35 m apart. From a point on the roof of building the angle of elevation of the top of statue is 24° and the angle of depression of base of the statue is 34°. Find the height of the statue. (tan 24° = 0.4452, tan 34° = 0.6745)
A portion of a 60 m long tree is broken by a tornado and the top struck up the ground making an angle of 30° with the ground level. The height of the point where the tree is broken is equal to ____________.
The angle of elevation of the top of a tower from two points distant s and t from its foot are complementary. Prove that the height of the tower is `sqrt(st)`
The angle of elevation of the top of a 15 m high tower at a point `15sqrt(3)` m away from the base of the tower is ______.
