Advertisements
Advertisements
Question
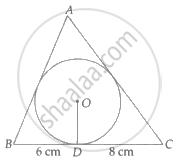
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 6 cm and 8 cm respectively. If the area of ΔABC is 84 cm2, find the lengths of sides AB and AC.
Solution
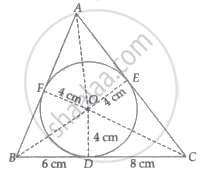
Given, BD = 6 cm, DC = 8 cm
Here, BD = BF and DC = CE .....[Tangents drawn from an external point to a circle are equal]
∴ BF = 6 cm and CE = 8 cm
Let AF = x = AE .....[Tangents drawn from external point A to the circle are equal]
In ΔABC,
a = BC = BD + DC = 6 + 8 = 14 cm
b = AC = CE + AE = (8 + x) cm
c = AB = BF + AF = (6 + x) cm
Now, s = `("a" + "b" + "c")/2`
= `(14 + (8 + "x") + (6 + "x"))/2`
= `(28 + 2"x")/2`
= (14 + x) cm
∴ Area of ΔABC = `sqrt("s"("s" - "a")("s" - "b")("s" - "c"))`
84 = `sqrt((14 + "x")(14 + "x" - 14)(14 + "x" - 8 - "x")(14 + "x" - 6 - "x"))`
84 = `sqrt("x"(14 + "x")(6)(8)`
84 = `sqrt(48"x"("x" + 14)) "cm"^2` ...(i)
`sqrt(48"x"("x" + 14))` = 84
On squaring both sides, we get
48x(x + 14) = 84 × 84
⇒ 4x(x + 14) = 84 × 7
⇒ x2 + 14x – 147 = 0
⇒ x2 + 21x – 7x – 147 = 0
x(x + 21) – 7(x + 21) = 0
(x + 21)(x – 7) = 0
So, x = 7, or x = –21 (rejected as - ve)
Hence, x = 7
Therefore, AB = c = 6 + x = 6 + 7 = 13 cm
AC = b = 8 + x = 8 + 7 = 15 cm
APPEARS IN
RELATED QUESTIONS
PQ is a tangent drawn from an external point P to a circle with centre O, QOR is the diameter of the circle. If ∠POR = 120°, what is the measure of ∠OPQ?
Prove that the centre of a circle touching two intersecting lines lies on the angle bisector of the lines.
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.

Find: ∠AOB
In the given figure PA = 6, PB = 4 and PC = 8. Find PD
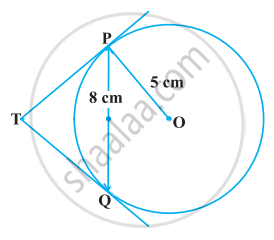
ln Figure, PQ is a chord of length 8 cm of a circle of radius 5 cm and centre O. The tangents at P and Q intersect at point T. find the length of TP.
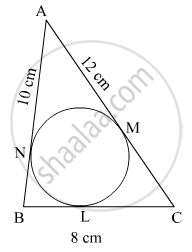
In Fig. 4, a circle is inscribed in a ΔABC having sides BC = 8 cm, AB = 10 cm and AC = 12 cm. Find the lengths BL, CM and AN.
The number of tangents drawn at a point of the circle is/are ______
The length of the tangent from an external point P on a circle with centre O is ______
In the given figure, PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q meet at a point T. Find the length of TP.

PA and PB are tangents drawn to a circle of centre O from an external point P. Chord AB makes an angle of 30° with the radius at the point of contact. If length of the chord is 6 cm, find the length of the tangent PA and the length of the radius OA.