Advertisements
Advertisements
Question
PQ is a tangent drawn from an external point P to a circle with centre O, QOR is the diameter of the circle. If ∠POR = 120°, what is the measure of ∠OPQ?
Solution
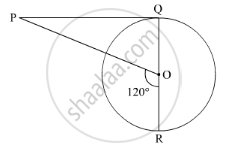
Given: PQ is the tangent to the circle with centre O. QOR is the diameter.
In\[∆ POQ\]
\[ \Rightarrow \angle OPQ = 120^o - 90^o = 30^o\]
APPEARS IN
RELATED QUESTIONS
In the following figure, Q is the centre of a circle and PM, PN are tangent segments to the circle. If ∠MPN = 50°, find ∠MQN.

Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
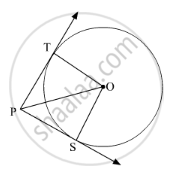
In Fig. 2, from a point P, two tangents PT and PS are drawn to a circle with centre O such that ∠SPT = 120°, Prove that OP = 2PS ?
Find the area of the shaded region in Fig. 8, where \\

Prove that the centre of a circle touching two intersecting lines lies on the angle bisector of the lines.
In the given circle with center o, ∠ABC=100°, ∠ACD=40° and CT is tangent to the circle at C. find ∠ADC and ∠DCT.

In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.

Find: ∠AOB
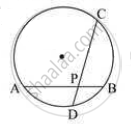
In the given figure PA = 6, PB = 4 and PC = 8. Find PD
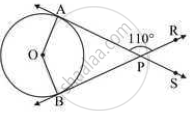
Find the angle between two radii at the centre of the circle as shown in the figure. Lines PA and PB are tangents to the circle at other ends of the radii and ∠APR = 110°.
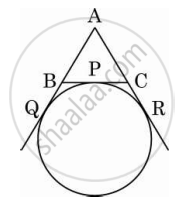
If a circle is touching the side BC of ΔABC at P and is touching AB and AC produced at Q and R respectively (see the figure). Prove that AQ = `1/2` (perimeter of ΔABC).