Advertisements
Advertisements
प्रश्न
PQ is a tangent drawn from an external point P to a circle with centre O, QOR is the diameter of the circle. If ∠POR = 120°, what is the measure of ∠OPQ?
उत्तर
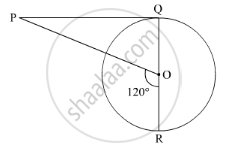
Given: PQ is the tangent to the circle with centre O. QOR is the diameter.
In\[∆ POQ\]
\[ \Rightarrow \angle OPQ = 120^o - 90^o = 30^o\]
APPEARS IN
संबंधित प्रश्न
Prove that a parallelogram circumscribing a circle is a rhombus.
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segments joining the points of contact to the centre.
In the following figure, PQ = QR, ∠RQP = 68°, PC and CQ are tangents to the circle with centre O.

Calculate the values of:
- ∠QOP
- ∠QCP
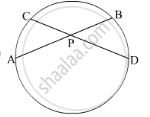
In the given figure PA = 10, PB = 2 and PC = 5. Find PD.
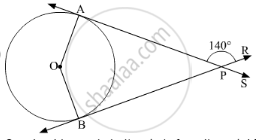
Find the angle between two radii at the centre of the circle as shown in the figure. Lines PA and PB are tangents to the circle at other ends of the radii and ∠APR = 140°.
In the given circle with center o, ∠ABC=100°, ∠ACD=40° and CT is tangent to the circle at C. find ∠ADC and ∠DCT.

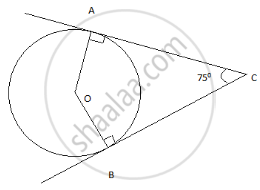
In fig, O is the centre of the circle, CA is tangent at A and CB is tangent at B drawn to the circle. If ∠ACB = 75°, then ∠AOB = ______
The angle between two tangents to a circle may be 0°.
The length of tangent from an external point P on a circle with centre O is always less than OP.
In the given figure, PA and PB are tangents from external point P to a circle with centre C and Q is any point on the circle. Then the measure of ∠AQB is ______.

