Advertisements
Advertisements
प्रश्न
State the AAA-similarity criterion
उत्तर
If the corresponding angles of two triangles are equal, then their corresponding sides are proportional and hence the triangles are similar.
APPEARS IN
संबंधित प्रश्न
CD and GH are, respectively, the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG, respectively. If ΔABC ~ ΔFEG, Show that
- `("CD")/("GH") = ("AC")/("FG")`
- ΔDCB ~ ΔHGE
- ΔDCA ~ ΔHGF
If AD and PM are medians of triangles ABC and PQR, respectively where ΔABC ~ ΔPQR, prove that `("AB")/("PQ") = ("AD")/("PM")`.
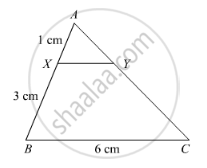
In the following figure, XY || BC. Find the length of XY.
Two triangles ABC and PQR are such that AB = 3 cm, AC = 6cm, ∠𝐴 = 70°, PR = 9cm ∠𝑃 = 70° and PQ = 4.5 cm. Show that ΔABC ∼ΔPQR and state that similarity criterion.
In ΔABC~ΔDEF such that 2AB = DE and BC = 6cm, find EF.
In a ∆PQR, PR2 – PQ2 = QR2 and M is a point on side PR such that QM ⊥ PR. Prove that QM2 = PM × MR.
In figure, two line segments AC and BD intersect each other at the point P such that PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° and ∠CDP = 30°. Then, ∠PBA is equal to ______.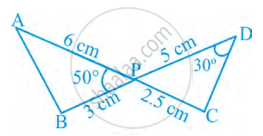
If in triangles ABC and DEF, `(AB)/(DE) = (BC)/(FD)`, then they will be similar, when ______.
In the given figure below, `(AD)/(AE) = (AC)/(BD)` and ∠1 = ∠2, Show that ΔBAE ∼ ΔCAD.

Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ΔPQR show that ΔABC ~ ΔPQR.