Advertisements
Advertisements
प्रश्न
Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
उत्तर
Consider the following pair of circles.
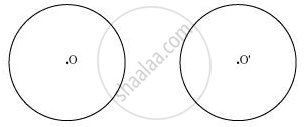
The above circles do not intersect each other at any point. Therefore, they do not have any point in common.
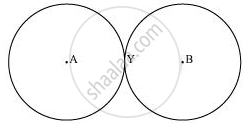
The above circles touch each other only at one point Y. Therefore, there is 1 point in common.
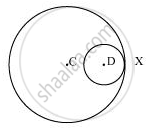
The above circles touch each other at 1 point X only. Therefore, the circles have 1 point in common.
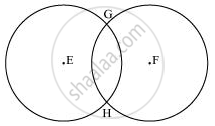
These circles intersect each other at two points G and H. Therefore, the circles have two points in common. It can be observed that there can be a maximum of 2 points in common. Consider the situation in which two congruent circles are superimposed on each other. This situation can be referred to as if we are drawing the circle two times.
APPEARS IN
संबंधित प्रश्न
Give a method to find the centre of a given circle.
A circular park of radius 40 m is situated in a colony. Three boys Ankur, Amit and Anand are sitting at equal distance on its boundary each having a toy telephone in his hands to talk
to each other.
Prove that any three points on a circle cannot be collinear.
Choose the correct alternative:
If the points, A, B, C are non-collinear points, then how many circles can be drawn which passes through points A, B, and C?
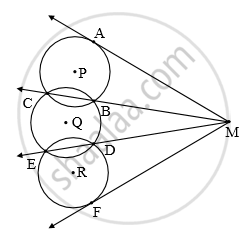
In the above figure, the circles with P, Q, and R intersect at points B, C, D, and E as shown. Lines CB and ED intersect in point M. Lines are drawn from point M to touch the circles at points A and F. Prove that MA = MF.
Four alternative answers for the following question is given. Choose the correct alternative.
How many circles can drawn passing through three non-collinear points?
How many circles can be drawn passing through a point?
Through three collinear points a circle can be drawn.
ABCD is such a quadrilateral that A is the centre of the circle passing through B, C and D. Prove that ∠CBD + ∠CDB = `1/2` ∠BAD
Find the value of y, if the points A(3, 4), B(6, y) and C(7, 8) are collinear.
