Advertisements
Advertisements
प्रश्न
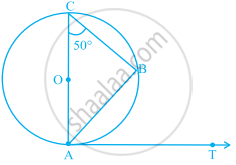
In figure, AB is a chord of the circle and AOC is its diameter such that ∠ACB = 50°. If AT is the tangent to the circle at point A, then ∠BAT is equal to ______.
विकल्प
65°
60°
50°
40°
उत्तर
In figure, AB is a chord of the circle and AOC is its diameter such that ∠ACB = 50°. If AT is the tangent to the circle at point A, then ∠BAT is equal to 50°.
Explanation:

In figure, AOC is a diameter of the circle.
We know that, diameter subtends an angle 90° at the circle.
So, ∠ABC = 90°
In ΔACB,
∠A + ∠B + ∠C = 180° ...[Since, sum of all angles of a triangle is 180°]
⇒ ∠A + 90° + 50° = 180°
⇒ ∠A + 140° = 180°
⇒ ∠A = 180° – 140° = 40°
∠A or ∠OAB = 40°
Now, AT is the tangent to the circle at point A.
So, OA is perpendicular to AT.
∴ ∠OAT = 90° ...[From figure]
⇒ ∠OAB + ∠BAT = 90°
On putting ∠OAB = 40°, we get
⇒ ∠BAT = 90° – 40° = 50°
Hence, the value of ∠BAT is 50°.
APPEARS IN
संबंधित प्रश्न
A circle touches the side BC of a ΔABC at a point P and touches AB and AC when produced at Q and R respectively. As shown in the figure that AQ = `1/2` (Perimeter of ΔABC).

In two concentric circles, prove that all chords of the outer circle which touch the inner circle are of equal length.
Fill in the blanks:
An arc is a __________ when its ends are the ends of a diameter.
In the given figure, BC is a tangent to the circle with centre O. OE bisects AP. Prove that ΔAEO~Δ ABC.

O is the centre of a circle of radius 10 cm. P is any point in the circle such that OP = 6 cm. A is the point travelling along the circumference. x is the distance from A to P. what are the least and the greatest values of x in cm? what is the position of the points O, P and A at these values?
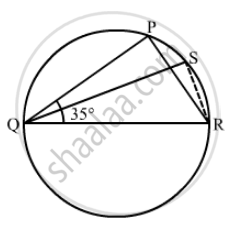
In the given figure, ΔPQR is an isosceles triangle with PQ = PR and m ∠PQR = 35°. Find m ∠QSR and m ∠QTR.
ABC is a triangle with B as right angle, AC = 5 cm and AB = 4 cm. A circle is drawn with Aas centre and AC as radius. The length of the chord of this circle passing through C and B is
Find the length of the chord of a circle in the following when:
Radius is 13 cm and the distance from the centre is 12 cm
In the figure, O is the center of the circle. Line AQ is a tangent. If OP = 3, m(arc PM) = 120°, then find the length of AP.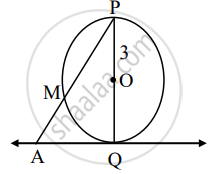
In the following figure, if OA = 5 cm, AB = 8 cm and OD is perpendicular to AB, then CD is equal to ______.