Advertisements
Advertisements
प्रश्न
PQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR. Show that PM2 = QM . MR
उत्तर
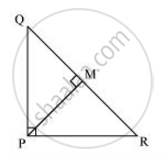
Let ∠MPR = x
In ΔMPR
∠MPR = 180º- 90º - x
∠MRP = 90º - x
Similarity, in ΔMPQ
∠MPQ = 90º - ∠MPR
= 90º - x
∠MQP = 180º - 90º - (90º - x)
∠MQP = x
In ΔQMP and ΔPMR
∠MPQ = ∠MRP
∠PMQ = ∠RMP
∠MQP = ∠MPR
∴ΔQMP ~ ΔPMR (By AAA Similarity criterion)
`=>(QM)/(PM) = (MP)/(MR)`
=>PM2 = QM x MR
APPEARS IN
संबंधित प्रश्न
ABC is a right-angled triangle, right-angled at A. A circle is inscribed in it. The lengths of the two sides containing the right angle are 5 cm and 12 cm. Find the radius of the circle
In the following figure, O is a point in the interior of a triangle ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that

(i) OA2 + OB2 + OC2 − OD2 − OE2 − OF2 = AF2 + BD2 + CE2
(ii) AF2 + BD2 + CE2 = AE2 + CD2 + BF2
Walls of two buildings on either side of a street are parallel to each other. A ladder 5.8 m long is placed on the street such that its top just reaches the window of a building at the height of 4 m. On turning the ladder over to the other side of the street, its top touches the window of the other building at a height 4.2 m. Find the width of the street.
If P and Q are the points on side CA and CB respectively of ΔABC, right angled at C, prove that (AQ2 + BP2 ) = (AB2 + PQ2)
Prove that in a right angle triangle, the square of the hypotenuse is equal to the sum of squares of the other two sides.
Find the length of the hypotenuse of a triangle whose other two sides are 24cm and 7cm.
A ladder 25m long reaches a window of a building 20m above the ground. Determine the distance of the foot of the ladder from the building.
Find the unknown side in the following triangles
A flag pole 18 m high casts a shadow 9.6 m long. Find the distance of the top of the pole from the far end of the shadow.
Two poles of 10 m and 15 m stand upright on a plane ground. If the distance between the tops is 13 m, find the distance between their feet.
