Advertisements
Advertisements
प्रश्न
ABCD is a rectangle whose three vertices are B (4, 0), C(4, 3) and D(0,3). The length of one of its diagonals is
(A) 5
(B) 4
(C) 3
(D) 25
उत्तर
Correct answer: A
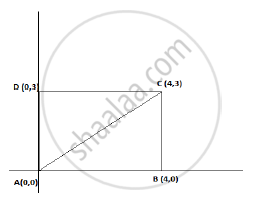
We see that AB = 4 units and BC = 3 units
Using Pythagoras theorem
AC2= AB2+ BC2
=42 + 32
AC 2 =25
Thus AC = 5 units
Hence length of the diagonal of the rectangle is 5 units
APPEARS IN
संबंधित प्रश्न
ABC is an equilateral triangle of side 2a. Find each of its altitudes.
In the given figure, point T is in the interior of rectangle PQRS, Prove that, TS2 + TQ2 = TP2 + TR2 (As shown in the figure, draw seg AB || side SR and A-T-B)

Digonals of parallelogram WXYZ intersect at point O. If OY =5, find WY.
In triangle ABC, angle A = 90o, CA = AB and D is the point on AB produced.
Prove that DC2 - BD2 = 2AB.AD.
ABC is a triangle, right-angled at B. M is a point on BC.
Prove that: AM2 + BC2 = AC2 + BM2
In triangle ABC, ∠B = 90o and D is the mid-point of BC.
Prove that: AC2 = AD2 + 3CD2.
In the figure below, find the value of 'x'.

The foot of a ladder is 6m away from a wall and its top reaches a window 8m above the ground. If the ladder is shifted in such a way that its foot is 8m away from the wall to what height does its tip reach?
From given figure, In ∆ABC, If AC = 12 cm. then AB =?

Activity: From given figure, In ∆ABC, ∠ABC = 90°, ∠ACB = 30°
∴ ∠BAC = `square`
∴ ∆ABC is 30° – 60° – 90° triangle
∴ In ∆ABC by property of 30° – 60° – 90° triangle.
∴ AB = `1/2` AC and `square` = `sqrt(3)/2` AC
∴ `square` = `1/2 xx 12` and BC = `sqrt(3)/2 xx 12`
∴ `square` = 6 and BC = `6sqrt(3)`
The perimeters of two similar triangles ABC and PQR are 60 cm and 36 cm respectively. If PQ = 9 cm, then AB equals ______.
