Advertisements
Advertisements
Question
A man goes 18 m due east and then 24 m due north. Find the distance of his current position from the starting point?
Solution
Let the initial position of the man be “O” and his final position be “B”.
By Pythagoras theorem
In the right ∆OAB,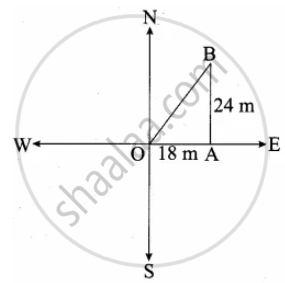
OB2 = OA2 + AB2
= 182 + 242
= 324 + 576 = 900
OB = `sqrt(900)` = 30
The distance of his current position is 30 m
APPEARS IN
RELATED QUESTIONS
A man goes 10 m due east and then 24 m due north. Find the distance from the starting point
ABC is a right-angled triangle, right-angled at A. A circle is inscribed in it. The lengths of the two sides containing the right angle are 5 cm and 12 cm. Find the radius of the circle
In triangle ABC, AB = AC and BD is perpendicular to AC.
Prove that: BD2 - CD2 = 2CD × AD
In triangle ABC, angle A = 90o, CA = AB and D is the point on AB produced.
Prove that DC2 - BD2 = 2AB.AD.
Prove that in a right angle triangle, the square of the hypotenuse is equal to the sum of squares of the other two sides.
Triangle XYZ is right-angled at vertex Z. Calculate the length of YZ, if XY = 13 cm and XZ = 12 cm.
A ladder, 6.5 m long, rests against a vertical wall. If the foot of the ladder is 2.5 m from the foot of the wall, find up to how much height does the ladder reach?
If in a ΔPQR, PR2 = PQ2 + QR2, then the right angle of ∆PQR is at the vertex ________
Jayanti takes shortest route to her home by walking diagonally across a rectangular park. The park measures 60 metres × 80 metres. How much shorter is the route across the park than the route around its edges?
Height of a pole is 8 m. Find the length of rope tied with its top from a point on the ground at a distance of 6 m from its bottom.
