Advertisements
Advertisements
Question
Pranali and Prasad started walking to the East and to the North respectively, from the same point and at the same speed. After 2 hours distance between them was \[15\sqrt{2}\]
km. Find their speed per hour.
Solution

It is given that, Pranali and Prasad have same speed.
Thus, they cover same distance in 2 hours.
i.e. OA = OB
Let the speed be x km per hour.
According to Pythagoras theorem,
In ∆AOB
\[{AB}^2 = {AO}^2 + {OB}^2 \]
\[ \Rightarrow \left( 15\sqrt{2} \right)^2 = {AO}^2 + {OA}^2 \]
\[ \Rightarrow 450 = 2 {AO}^2 \]
\[ \Rightarrow {AO}^2 = \frac{450}{2}\]
\[ \Rightarrow {AO}^2 = 225\]
\[ \Rightarrow AO = 15 km\]
\[ \Rightarrow BO = 15 km\]
\[\text{Speed} = \frac{Distance}{Time}\]
\[ = \frac{15}{2}\]
\[ = 7 . 5 \text{km per hour}\]
APPEARS IN
RELATED QUESTIONS
The points A(4, 7), B(p, 3) and C(7, 3) are the vertices of a right traingle ,right-angled at B. Find the values of p.
Tick the correct answer and justify: In ΔABC, AB = `6sqrt3` cm, AC = 12 cm and BC = 6 cm.
The angle B is:
ABC is a triangle right angled at C. If AB = 25 cm and AC = 7 cm, find BC.
Identify, with reason, if the following is a Pythagorean triplet.
(24, 70, 74)
In triangle ABC, AB = AC = x, BC = 10 cm and the area of the triangle is 60 cm2.
Find x.
In an isosceles triangle ABC; AB = AC and D is the point on BC produced.
Prove that: AD2 = AC2 + BD.CD.
In the following Figure ∠ACB= 90° and CD ⊥ AB, prove that CD2 = BD × AD

In triangle PQR, angle Q = 90°, find: PQ, if PR = 34 cm and QR = 30 cm
Show that the triangle ABC is a right-angled triangle; if: AB = 9 cm, BC = 40 cm and AC = 41 cm
A right triangle has hypotenuse p cm and one side q cm. If p - q = 1, find the length of third side of the triangle.
A ladder 15m long reaches a window which is 9m above the ground on one side of a street. Keeping its foot at the same point, the ladder is turned to other side of the street to reach a window 12m high. Find the width of the street.
From a point O in the interior of aΔABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: AF2 + BD2 + CE2 = AE2 + CD2 + BF2
In a triangle ABC right angled at C, P and Q are points of sides CA and CB respectively, which divide these sides the ratio 2 : 1.
Prove that: 9BP2 = 9BC2 + 4AC2
In a right-angled triangle ABC,ABC = 90°, AC = 10 cm, BC = 6 cm and BC produced to D such CD = 9 cm. Find the length of AD.
Determine whether the triangle whose lengths of sides are 3 cm, 4 cm, 5 cm is a right-angled triangle.
Find the unknown side in the following triangles
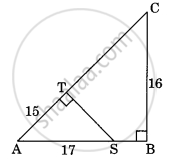
In the given figure, ∠T and ∠B are right angles. If the length of AT, BC and AS (in centimeters) are 15, 16, and 17 respectively, then the length of TC (in centimeters) is ______.
In an equilateral triangle PQR, prove that PS2 = 3(QS)2.

If the areas of two circles are the same, they are congruent.
The foot of a ladder is 6 m away from its wall and its top reaches a window 8 m above the ground. Find the length of the ladder.
