Advertisements
Advertisements
प्रश्न
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If `"AD"/"DB"=2/3` and AC = 18 cm, find AE
उत्तर

We have,
`"AD"/"DB"=2/3`and DE || BC
Therefore, by basic proportionality theorem, we have
`"AD"/"DB"="EC"/"AE"`
`rArr3/2="EC"/"AE"`
Adding 1 on both sides, we get
`rArr3/2+1="EC"/"AE"+1`
`rArr(3+2)/2=("EC"+"AE")/"AE"`
`rArr5/2="AC"/"AE"` [∵ AE + EC = AC]
`rArr5/2=18/"AE"` [∵ AC = 18]
`rArr"AE=(18xx2)/5"`
`rArr"AE"=36/5=7.2 " cm"`
APPEARS IN
संबंधित प्रश्न
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 2.5 cm, BD = 3.0 cm and AE = 3.75 cm, find the length of AC.
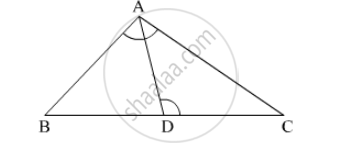
ΔABC is an isosceles triangle with AB = AC = 13cm. The length of altitude from A on BC is 5cm. Find BC.
In the given figure, D is the midpoint of side BC and AE⊥BC. If BC = a, AC = b, AB = c, AD = p and AE = h, prove that
(i)`B^2=p^2+ax+a^2/x`
(ii)` c^2=p^2-ax+a^2/x`
(iii) `b^2+c^2=2p^2+a^2/2`
(iv)`b^2-c^2=2ax`

In ΔABC, AB = AC. Side BC is produced to D. Prove that `AD^2−AC^2`= BD.CD
◻ABCD is a parallelogram point E is on side BC. Line DE intersects ray AB in point T. Prove that DE × BE = CE × TE.

In the given figure, in ∆ABC, point D on side BC is such that, ∠BAC = ∠ADC. Prove that, CA2 = CB × CD
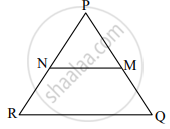
In ΔPQR, NM || RQ. If PM = 15, MQ = 10, NR = 8, then find PN.
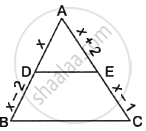
In fig, seg DE || sec BC, identify the correct statement.

In ΔABC, AB = 6 cm and DE || BC such that AE = `1/4` AC then the length of AD is ______.
In the given figure, ABC is a triangle in which DE||BC. If AD = x, DB = x – 2, AE = x + 2 and EC = x – 1, then find the value of x.