Question

InΔ  ABC , M and N are points on the sides AB and AC respectively such that BM= CN. If ∠B = ∠C then show that MN||BC  

Answer 1

 

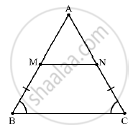
In ΔABC, ∠B = ∠ 𝐶 

∴ AB = AC (Sides opposite to equal angle are equal)
Subtracting BM from both sides, we get  

AB – BM = AC – BM
⟹AB – BM = AC – CN (∵BM =CN)
⟹AM =AN
∴∠AMN =∠ ANM (Angles opposite to equal sides are equal)
Now, in ΔABC,
∠𝐴+ ∠B + ∠C =180°   ----(1)  (Angle Sum Property of triangle)  

Again In In ΔAMN,
∠A + ∠AMN + ∠ ANM =180° ----(2)
(Angle Sum Property of triangle)
From (1) and (2), we get
∠B + ∠ C = ∠ AMN + ∠ ANM
⟹ 2∠B = 2∠ AMN 
⟹∠B = ∠ AMN
Since, ∠B and ∠ AMN are corresponding angles.
∴ MN ‖ BC.