Advertisements
Advertisements
рдкреНрд░рд╢реНрди
A guy wire attached to a vertical pole of height 18 m is 24m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
рдЙрддреНрддрд░
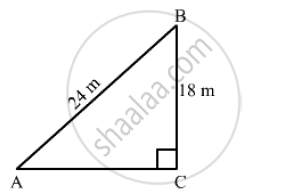
Let AB be a guy wire attached to a pole BC of height 18 m. Now, to keep the wire taut let it to be fixed at A.
Now, In right triangle ABC
By using Pythagoras theorem, we have
`AB^2=BC^2+CA^2`
⇒ `24^2=18^2+CA^2`
`⇒ CA^2=576-324`
`⇒ CA^2=252`
`⇒ CA=6sqrt7` m
Hence, the stake should be driven` 6 sqrt7`ЁЭСЪ far from the base of the pole.
APPEARS IN
рд╕рдВрдмрдВрдзрд┐рдд рдкреНрд░рд╢реНрди
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If `"AD"/"DB"=3/4` and AC = 15 cm, find AE
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 4, AE = 8, DB = x – 4, and EC = 3x – 19, find x.
In ΔABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 8x − 7, DB = 5x − 3, AE = 4x − 3 and EC = (3x − 1), find the value of x.
D and E are points on the sides AB and AC respectively of a ΔABC such that DEтХСBC.
If AB = 13.3cm, AC = 11.9cm and EC = 5.1cm, find AD.
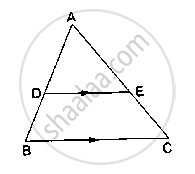
D and E are points on the sides AB and AC respectively of a ΔABC such that DEтХСBC. Find the value of x, when
AD = (7x – 4) cm, AE = (5x – 2) cm, DB = (3x + 4) cm and EC = 3x cm.
ΔABC is an isosceles triangle with AB = AC = 13cm. The length of altitude from A on BC is 5cm. Find BC.
Find the length of altitude AD of an isosceles ΔABC in which AB = AC = 2a units and BC = a units.
State the basic proportionality theorem.
In the given figure, in тИЖABC, point D on side BC is such that, ∠BAC = ∠ADC. Prove that, CA2 = CB × CD
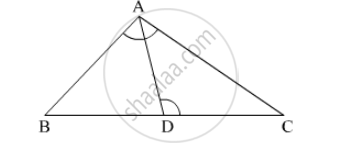
Prove that If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio. In the figure, find EC if `(AD)/(DB) = (AE)/(EC)` using the above theorem.
