Advertisements
Advertisements
Question
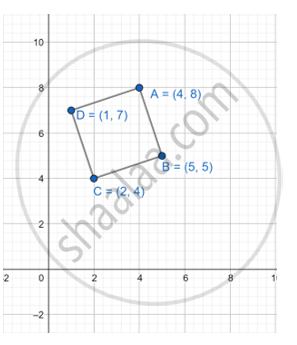
Show that ABCD is a parallelogram if A = (4, 8), B = (5, 5), C = (2, 4), D = (1, 7)
Solution
Given: A = (4, 8), B = (5, 5), C = (2, 4), D = (1, 7)
To Prove: AD || BC
AB || DC
Proof:
Let A (4,8) = (x1, y1); B (5,5) = (x2, y2);
C (2,4) = (x3, y3) and D (1,7) = (x4, y4)
Distance between two points P (x1, y1) and Q (x2, y2) = `("y"_2-"y"_1)/("x"_2-"x"_1)`
The slope of the line AB= `("y"_2-"y"_1)/("x"_2-"x"_1)` [Distance formula]
=`(5-8)/(5-4)`
=`-3/1=-3` .........(i)
The slope of the line DC = `("y"_4-"y"_3)/("x"_4-"x"_3)` = [Distance formula]
=`(7-4)/(1-2)`
=`3/(-1)=-3` ..........(ii)
The slope of the line AD=`("y"_4-"y"_1)/("x"_2-"x"_1)` = [Distance formula]
= `(7-4)/(1-4)`
= `(-1)/-3 = 1/3` ............(iii)
The slope of the line BC=`("y"_3-"y"_2)/("x"_3-"x"_2)` = [Distance formula]
=`(4-5)/(2-5)=(-1)/(-3) =1/3`
The slope of line AB = The slope od’s the line DC [From (1) and (2)]
∴ AB || DC
The slope of line AD = The slope of the line BC [From(3) and (4)]
∴ AD || BC
Hence, ABCD is a parallelogram.
APPEARS IN
RELATED QUESTIONS
If P(-2,4), Q(4,8), R(10, 5) and S(4, 1) are the vertices of a quadrilateral, show that it is a parallelogram.
In figure ∠ABC = 120°, where A, B and C are points on the circle with centre O. Find ∠OAC?
`square`ABCD is cyclic. If ∠B = 110°, then find measure of ∠D.
In figure, points G, D, E, F are concyclic points of a circle with centre C.
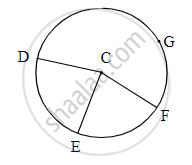
∠ECF = 70°, m(arc DGF) = 200°
Find m(arc DEF) by completing activity.
m(arc EF) = ∠ECF ......[Definition of measure of arc]
∴ m(arc EF) = `square`
But; m(arc DE) + m(arc EF) + m(arc DGF) = `square` .....[Measure of a complete circle]
∴ m(arc DE) = `square`
∴ m(arc DEF) = m(arc DE) + m(arc EF)
∴ m(arc DEF) = `square`
Two opposite angles of a parallelogram are (2x + 60)° and (4x)°. Find the value of x.
