Advertisements
Advertisements
Question
If P(-2,4), Q(4,8), R(10, 5) and S(4, 1) are the vertices of a quadrilateral, show that it is a parallelogram.
Solution
To prove: PQRS is a parallelogram.
The quadrilateral is a parallelogram if opposite sides of quadrilateral are equal in length and parallel to each other
Consider PS and QR as opposite sides of quadrilateral
And PQ and RS as opposite sides of quadrilateral
The slope of a line is given by `(y_2 - y_1)/(x_2 - x_1)` where `(x_1,y_1) & (x_2,y_2)` are points on line
Checking for PS and QR
the slope of PS = `(1 - 4)/(4 - (-2)) = (-3)/6 = -1/2`
slope of QR = `(5 - 8)/(10 - 4) = (-3)/6 = -1/2`
Slope of PS = Slope of QR…(i)
Therefore, PS parallel to QR
Length of PS using distance formula
`"PS" = sqrt((4 - (-2))^2 + (1 - 4)^ = sqrt(36 + 9) = sqrt(9 xx 5) = 3sqrt(5)
Length of QR
`"QR" = sqrt((10 - 4)^2 + (5 - 8)^2) = sqrt(36 + 9) = sqrt(9 xx 5) = 3sqrt(5)`
Length of PS = Length of QR…(ii)
Checking for PQ and RS
Slope pf PQ = `(8 - 4)/(4 - (-2)) = 4/6 = 2/3`
Slope of RS = `(1 - 5)/(4 - 10) = (-4)/(-6) = 2/3`
Slope of PQ = Slope of RS…(iii)
Therefore, PQ parallel to RS
Length of PQ using distance formula
`"PQ" = sqrt((4 - (-2))^2 + (8-4)^2) = sqrt(36 + 16) = sqrt(52)`
Length of RS
`"QR" = sqrt((4 - 10)^2 + (1 - 5)^2) = sqrt(36 + 16) = sqrt(52)`
Length of PQ = Length of RS…(iv)
Using equations (i),(ii),(iii) and (iv) we conclude that quadrilateral PQRS is a parallelogram
Hence proved
APPEARS IN
RELATED QUESTIONS
Show that ABCD is a parallelogram if A = (4, 8), B = (5, 5), C = (2, 4), D = (1, 7)
In figure ∠ABC = 120°, where A, B and C are points on the circle with centre O. Find ∠OAC?
`square`ABCD is cyclic. If ∠B = 110°, then find measure of ∠D.
In figure, points G, D, E, F are concyclic points of a circle with centre C.
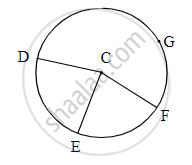
∠ECF = 70°, m(arc DGF) = 200°
Find m(arc DEF) by completing activity.
m(arc EF) = ∠ECF ......[Definition of measure of arc]
∴ m(arc EF) = `square`
But; m(arc DE) + m(arc EF) + m(arc DGF) = `square` .....[Measure of a complete circle]
∴ m(arc DE) = `square`
∴ m(arc DEF) = m(arc DE) + m(arc EF)
∴ m(arc DEF) = `square`
Two opposite angles of a parallelogram are (2x + 60)° and (4x)°. Find the value of x.
