Question

In figure, points G, D, E, F are concyclic points of a circle with centre C.

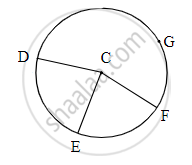
∠ECF = 70°, m(arc DGF) = 200°

Find m(arc DEF) by completing activity.

m(arc EF) = ∠ECF   ...[Definition of measure of arc]

∴ m(arc EF) = `square`

But; m(arc DE) + m(arc EF) + m(arc DGF) = `square`   ...[Measure of a complete circle]

∴ m(arc DE) = `square`

∴ m(arc DEF) = m(arc DE) + m(arc EF)

∴ m(arc DEF) = `square`

Answer 1

m(arc EF) = ∠ECF   ...[Definition of measure of arc]

∴ m(arc EF) = \[\boxed{70°}\]      ...(i)

But; m(arc DE)+ m(arc EF) + m(arc DGF) = \[\boxed{360°}\]   ...[Measure of a complete circle]

∴ m(arc DE) + 70° + 200° = 360°

m(arc DE) = 360° – 270°   ...[From (i) and given]

∴ m(arc DE) = \[\boxed{90°}\]   ...(ii)

∴ m(arc DEF) = m(arc DE) + m(arc EF)

= 90° + 70°   ...[From (i) and (ii)]

∴ m(arc DEF) = \[\boxed{160°}\]