Advertisements
Advertisements
प्रश्न
ΔABC ~ ΔDEF and their areas are respectively `100cm^2` and `49cm2`. If the altitude of ΔABC is 5cm, find the corresponding altitude of ΔDEF.
उत्तर
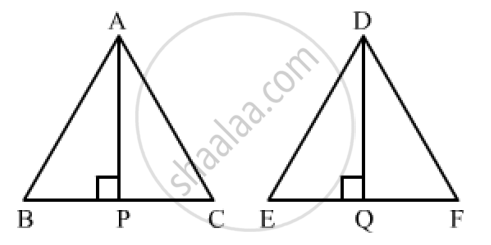
It is given that ΔABC ~ ΔDEF.
Therefore, the ration of the areas of these triangles will be equal to the ratio of squares of their corresponding sides.
Also, the ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding altitudes.
Let the altitude of ΔABC be AP, drawn from A to BC to meet BC at P and the altitude of ΔDEF be DQ, drawn from D to meet EF at Q.
`(ar(Δ ABC))/(ar(ΔDEF))=(AP^2)/(DQ^2)`
⇒` 100/49=5^2/(DQ^2)`
⇒ `100/49=25/(DQ^2)`
⇒ `DQ^2=(49xx25)/100`
⇒`DQ=sqrt((49xx25)/100)`
⟹ 𝐷𝑄=3.5 𝑐𝑚
Hence, the altitude of ΔDEF is 3.5 cm
APPEARS IN
संबंधित प्रश्न
In the figure given below, Ray PT is bisector of ∠QPR. If PQ = 5.6 cm, QT = 4 cm and TR = 5 cm, find the value of x .

D is a point on the side BC of ∆ABC such that ∠ADC = ∠BAC. Prove that` \frac{"CA"}{"CD"}=\frac{"CB"}{"CA"} or "CA"^2 = "CB" × "CD".`
The diagonal BD of a parallelogram ABCD intersects the segment AE at the point F, where E is any point on the side BC. Prove that DF × EF = FB × FA
Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting AC in L and AD produced in E. Prove that EL = 2 BL
See the given figure. DE || BC. Find AD.

In the given figure, two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that
(i) ΔPAC ∼ ΔPDB
(ii) PA.PB = PC.PD

ΔABC~ΔPQR and ar(ΔABC) = 4, ar(ΔPQR) . If BC = 12cm, find QR.
State the AA-similarity criterion
State the SAS-similarity criterion
If in ∆DEF and ∆PQR, ∠D ≅ ∠Q, ∠R ≅ ∠E then which of the following statements is false?

In the given figure, seg XY || seg BC, then which of the following statements is true?

A triangle ABC is enlarged, about the point O as centre of enlargement, and the scale factor is 3. Find : OA, if OA' = 6 cm.
A model of a ship is made to a scale 1 : 300.
- The length of the model of the ship is 2 m. Calculate the length of the ship.
- The area of the deck of the ship is 180,000 m2. Calculate the area of the deck of the model.
- The volume of the model is 6.5 m3. Calculate the volume of the ship.
In the following figure, point D divides AB in the ratio 3 : 5. Find :
- `(AE)/(EC)`
- `(AD)/(AB)`
- `(AE)/(AC)`
Also, if: - DE = 2.4 cm, find the length of BC.
- BC = 4.8 cm, find the length of DE.

In the given figure, PQ || AB; CQ = 4.8 cm QB = 3.6 cm and AB = 6.3 cm. Find : PQ

In the figure, given below, PQR is a right-angle triangle right angled at Q. XY is parallel to QR, PQ = 6 cm, PY = 4 cm and PX : XQ = 1 : 2. Calculate the lengths of PR and QR.

In the adjoining figure, the medians BD and CE of a ∆ABC meet at G. Prove that
(i) ∆EGD ∼ ∆CGB and
(ii) BG = 2GD for (i) above.
In the figure, DE || AC and DC || AP. Prove that `"BE"/"EC" = "BC"/"CP"`
The areas of two similar triangles are 169cm2 and 121cm2 respectively. If one side of the larger triangle is 26cm, find the length of the corresponding side of the smaller triangle.
A model of a ship is made to a scale of 1:500. Find: The volume of the model when the volume of the ship is 1km3
On a map drawn to a scale of 1:25000, a rectangular plot of land has sides 12cm x 16cm. Calculate: The diagonal distance of the plot in km
Check whether the triangles are similar and find the value of x
In the adjacent figure, ∆ABC is right angled at C and DE ⊥ AB. Prove that ∆ABC ~ ∆ADE and hence find the lengths of AE and DE
Construct a triangle similar to a given triangle PQR with its sides equal to `7/3` of the corresponding sides of the triangle PQR (scale factor `7/3 > 1`)
Two similar triangles will always have ________ angles
In figure, if AD = 6 cm, DB = 9 cm, AE = 8 cm and EC = 12 cm and ∠ADE = 48°. Find ∠ABC.

In the adjoining diagram the length of PR is ______.

