Question

Amrita stood near the base of a lighthouse, gazing up at its towering height. She measured the angle of elevation to the top and found it to be 60°. Then she climbed a nearby observation deck. 40 metres higher than her original position and noticed the angle of elevation to the top of lighthouse to be 45°.

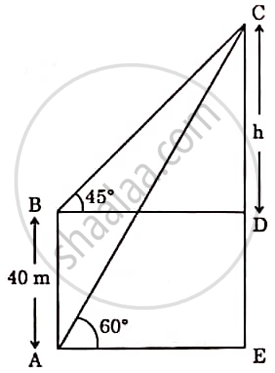
Based on the above given information, answer the following questions:

(i) If CD is h metres, find the distance BD in terms of 'h'. 

(ii) Find distance BC in terms of 'h'.

(iii) (a) Find the height CE of the lighthouse [Use `sqrt3` = 1.73]

OR 

(iii) (b) Find distance AE, if AC = 100m.

Answer 1

(i) From the right-angled triangle BDC: 

`tan 45^@ = h/"BD"`

Since tan⁡ 45° = 1, we get

`1 = h/"BD"`

BD = h

(ii) From the right-angled triangle ABC: 

`tan 60^@ = (BC)/(AE)`

Since tan⁡ 60° = `sqrt3`, we get:

`sqrt3 = (BC)/(AE)`

`BC = sqrt3 xx AE`

BC = BD + 40

BC = h + 40

h + 40 = `sqrt3 xx AE`

(iii) (a) Since CE + BC + h, substituting BC = h + 40:

CE = (h + 40) + h

CE = 2h + 40

To find h, we use: 

h + 40 = 1.73 × AE

h = 1.73AE − 40

From (i) BD = h, using triangle BDC: 

h = AE

CE = 2(AE) + 40

If AE = 100 (from part (iii) (b)):

CE = 2(100) + 40

CE = 240 meters

OR

(iii) (b) From the right triangle ACD: 

`tan 60^@ = (CD)/(AE)`

`sqrt3 = (h + 40)/(AE)`

`AE = (h + 40)/(sqrt3)`

If AC = 100, using Pythagoras Theorem in ACD:

AC² = AE² + CD²

Substituting values,

100² = AE² + (h + 40)²

`10000 = ((h + 40)/(sqrt3))^2 + (h + 40)^2`

`10000 = ((h + 40)^2)/(3) + (h + 40)^2`

`10000 = (4(h + 40)^2)/(3) + (3(h + 40)^2)/(3)`

`10000 = (4(h + 40)^2)/(3)`

Multiplying both sides by `3/4`

`3/4 xx 10000 = (h + 40)^2`

7500 = (h + 40)²

Taking the square root on both sides: 

`h + 40 = sqrt7500`

h + 40 = 86.6

h = 46.6

AE = `(h + 40)/(sqrt3)`

AE = `(86.6)/(1.73)`

AE = 50