Advertisements
Advertisements
Question
In the following figure, a quadrilateral LMNO circumscribes a circle with centre C. ∠O = 90°, LM = 25 cm, LO = 27 cm and MJ = 6 cm. Calculate the radius of the circle.

Solution
Given: ∠O = 90°, LM = 25 cm, LO = 27 cm, MJ = 6 cm
Tangents drawn from an exterior point to a circle have the same radius.
So, LI = LH
MI = MJ
NJ = NG
And OH = OG
Now, MI = MJ = 6 cm ......[Given]
So, LI = LM – MI
= 25 – 6
= 19 cm
So, LI = LH = 19 cm
Similarly, OH = LO – LH
= 27 – 19
= 8 cm
The tangent to a circle is perpendicular to the radius through the point of contact.
So, ∠CHO = ∠CGO = 90°
Also, ∠O = 90° ......[Given]
So, ∠GCH = 90°
As a result, CHOG is a square.
So, CH = CG = OH = 8 cm
As a result, the radius of the circle is 8 cm.
APPEARS IN
RELATED QUESTIONS
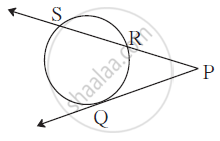
In the figure Q is the contact point. If
PQ = 12, PR = 8, then PS = ?
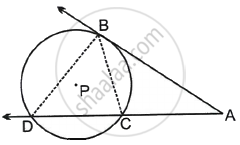
Given: In the figure, point A is in the exterior of the circle with centre P. AB is the tangent segment and secant through A intersects the circle in C and D.
To prove: AB2 = AC × AD
Construction: Draw segments BC and BD.
Write the proof by completing the activity.
Proof: In ΔABC and ΔADB,
∠BAC ≅ ∠DAB .....becuase ______
∠______ ≅ ∠______ ......[Theorem of tangent secant]
∴ ΔABC ∼ ΔADB .......By ______ test
∴ `square/square = square/square` .....[C.S.S.T.]
∴ AB2 = AC × AD
Proved.
