Advertisements
Advertisements
प्रश्न
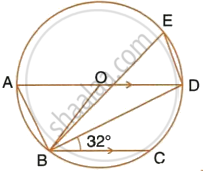
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.
Find:
- ∠OBD
- ∠AOB
- ∠BED
उत्तर
i. AD is parallel to BC, i.e., OD is parallel to BC and BD is transversal
`=>` ∠ODB = ∠CBD = 32° ...(Alternate angles)
In ΔOBD,
OD = OB ...(Radii of the same circle)
`=>` ∠ODB = ∠OBD = 32°
ii. AD is parallel to BC, i.e., AO is parallel to BC and OB is transversal.
`=>` ∠AOB = ∠OBC ...(Alternate angles)
`=>` ∠OBC = ∠OBD + ∠DBC
`=>` ∠OBC = 32° + 32°
`=>` ∠OBC = 64°
`=>` ∠AOB = 64°
iii. In ΔOAB,
OA = OB ...(Radii of the same circle)
`=>` ∠OAB = ∠OBA = x ...(say)
`=>` ∠OAB + ∠OBA + ∠AOB = 180°
`=>` x + x + 64° = 180°
`=>` 2x = 180° – 64°
`=>` 2x = 116°
`=>` x = 58°
`=>` ∠OAB = 58°
i.e. ∠DAB = 58°
`=>` ∠DAB = ∠BED = 58° ...(Angles inscribed in the same arc are equal)
APPEARS IN
संबंधित प्रश्न
In the given figure, XY and X’Y’ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X’Y’ at B. Prove that ∠AOB = 90°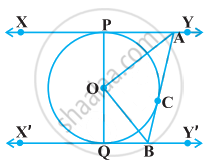
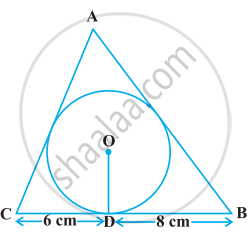
A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively (see given figure). Find the sides AB and AC.
Prove that the centre of a circle touching two intersecting lines lies on the angle bisector of the lines.
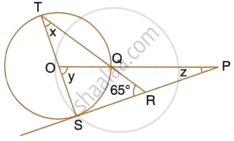
In the figure given below, O is the center of the circle and SP is a tangent. If ∠SRT = 65°, find the value of x, y and Z.
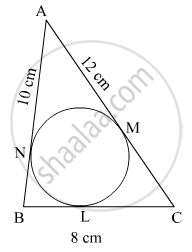
In Fig. 4, a circle is inscribed in a ΔABC having sides BC = 8 cm, AB = 10 cm and AC = 12 cm. Find the lengths BL, CM and AN.
Two concentric circles of radii a and b (a > b) are given. Find the length of the chord of the larger circle which touches the smaller circle.
The length of tangent from an external point P on a circle with centre O is always less than OP.
Two tangents PQ and PR are drawn from an external point to a circle with centre O. Prove that QORP is a cyclic quadrilateral.
In the given figure, there are two concentric circles with centre O. If ARC and AQB are tangents to the smaller circle from the point A lying on the larger circle, find the length of AC, if AQ = 5 cm.

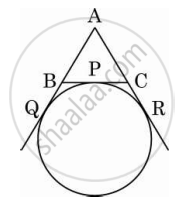
If a circle is touching the side BC of ΔABC at P and is touching AB and AC produced at Q and R respectively (see the figure). Prove that AQ = `1/2` (perimeter of ΔABC).