Advertisements
Advertisements
प्रश्न
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.

Find: ∠AOB
उत्तर
AD is parallel to BC, i.e., AO is parallel to BC and OB is transversal.
⇒ ∠ AOB = ∠ OBC ......(Alternate angles)
⇒ ∠ OBC = ∠ OBD + ∠ DBC
⇒ ∠OBC = 32° + 32°
⇒ ∠OBC = 64°
⇒ ∠ AOB = 64°
APPEARS IN
संबंधित प्रश्न
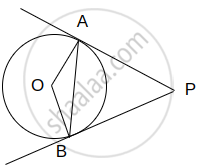
In the below given figure, two tangents RQ and RP are drawn from an external point R to the circle with centre O. If∠PRQ = 120°, then prove that OR = PR + RQ.

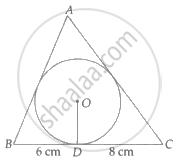
A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively (see given figure). Find the sides AB and AC.
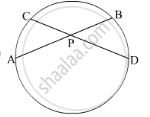
In the given figure PA = 10, PB = 2 and PC = 5. Find PD.
Find the area of the shaded region in Fig. 8, where \\

Prove that the centre of a circle touching two intersecting lines lies on the angle bisector of the lines.
A tangent is drawn from a point at a distance of 17 cm of circle C(0, r) of radius 8 cm. The length of its tangent is ______
The length of tangent from an external point P on a circle with centre O is always less than OP.
In the given figure, there are two concentric circles with centre O. If ARC and AQB are tangents to the smaller circle from the point A lying on the larger circle, find the length of AC, if AQ = 5 cm.

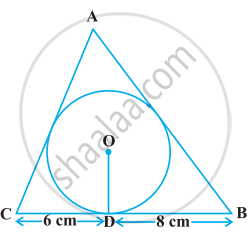
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 6 cm and 8 cm respectively. If the area of ΔABC is 84 cm2, find the lengths of sides AB and AC.
PA and PB are tangents drawn to a circle of centre O from an external point P. Chord AB makes an angle of 30° with the radius at the point of contact. If length of the chord is 6 cm, find the length of the tangent PA and the length of the radius OA.