Advertisements
Advertisements
प्रश्न
Two concentric circles of radii a and b (a > b) are given. Find the length of the chord of the larger circle which touches the smaller circle.
उत्तर
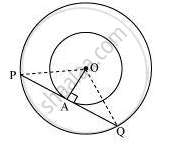
Let the two concentric circles be centered at point O.
Also, a > b where a is the radius of a larger circle and b is the radius of the smaller circle.
And let PQ be the chord of the larger circle which touches the smaller circle at point A. Therefore, PQ is tangent to the smaller circle.
OA ⊥ PQ (As OA is the radius of the circle)
Applying Pythagoras theorem in ΔOAP, we obtain
OA2+AP2=OP2
b2 + PA2 = a2
⇒ PA2 = a2 - b2
⇒ PA = `sqrt("a"^2-"b"^2)`
In ΔOPQ,
Since OA ⊥ PQ,
PA = AQ (Perpendicular from the center of the circle to the chord bisects the chord)
∴ PQ =2PA = `2sqrt("a"^2-"b"^2)`
Therefore, the length of the chord of the larger circle is `2sqrt("a"^2-"b"^2)` cm
APPEARS IN
संबंधित प्रश्न
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segments joining the points of contact to the centre.
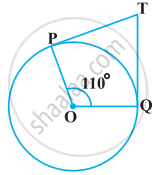
In the given figure, if TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to ______.
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
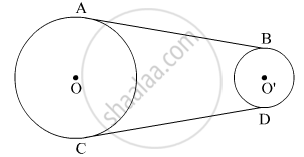
In the figure, AB and CD are common tangents to two circles of unequal radii. Prove that AB = CD.
PQ is a tangent drawn from an external point P to a circle with centre O, QOR is the diameter of the circle. If ∠POR = 120°, what is the measure of ∠OPQ?
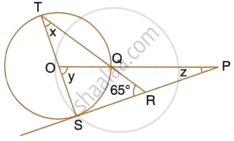
In the figure given below, O is the center of the circle and SP is a tangent. If ∠SRT = 65°, find the value of x, y and Z.
The length of tangents drawn from an external point to the circle ______
The number of tangents drawn at a point of the circle is/are ______
From an external point P, two tangents, PA and PB are drawn to a circle with centre O. At one point E on the circle tangent is drawn which intersects PA and PB at C and D, respectively. If PA = 10 cm, find the the perimeter of the triangle PCD.
From an external point, two tangents are drawn to a circle. Prove that the line joining the external point to the centre of the circle bisects the angle between the two tangents.
