Advertisements
Advertisements
Question
If from an external point B of a circle with centre O, two tangents BC and BD are drawn such that ∠DBC = 120°, prove that BC + BD = BO, i.e., BO = 2BC.
Solution

To prove: BO = 2BC
Given, ∠DBC = 120°
Join OC, OD and BO.
Since, BC and BD are tangents.
∴ OC ⊥ BC and OD ⊥ BD
We know, OB is the angle bisector of ∠DBC.
∴ ∠OBC = ∠DBO = 60°
In right-angled ∆OBC,
cos 60° = `("BC")/("OB")`
⇒ `1/2 = ("BC")/("OB")`
⇒ OB = 2 BC
Also, BC = BD ...[Tangent drawn from external point to circle are equal]
OB = BC + BC
⇒ OB = BC + BD
APPEARS IN
RELATED QUESTIONS
Prove that a parallelogram circumscribing a circle is a rhombus.
From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is ______.
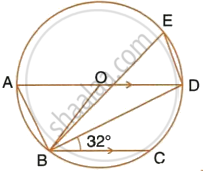
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.
Find:
- ∠OBD
- ∠AOB
- ∠BED
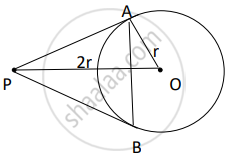
If two tangents inclined at an angle of 60° are drawn to a circle of radius 3 cm the length of each tangent is equal to ______
The number of tangents drawn at a point of the circle is/are ______
The length of tangent from an external point P on a circle with centre O is always less than OP.
From a point P, two tangents PA and PB are drawn to a circle C(0, r). If OP = 2r, then find ∠APB. What type of triangle is APB?
Two concentric circles with centre O are of radii 3 cm and 5 cm. Find the length of chord AB of the larger circle which touches the smaller circle at P.

PA and PB are tangents drawn to the circle with centre O as shown in the figure. Prove that ∠APB = 2∠OAB.

In the given diagram, O is the centre of the circle. PR and PT are two tangents drawn from the external point P and touching the circle at Q and S respectively. MN is a diameter of the circle. Given ∠PQM = 42° and ∠PSM = 25°.
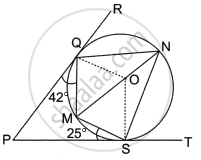
Find:
- ∠OQM
- ∠QNS
- ∠QOS
- ∠QMS
