Advertisements
Advertisements
प्रश्न
If from an external point B of a circle with centre O, two tangents BC and BD are drawn such that ∠DBC = 120°, prove that BC + BD = BO, i.e., BO = 2BC.
उत्तर

To prove: BO = 2BC
Given, ∠DBC = 120°
Join OC, OD and BO.
Since, BC and BD are tangents.
∴ OC ⊥ BC and OD ⊥ BD
We know, OB is the angle bisector of ∠DBC.
∴ ∠OBC = ∠DBO = 60°
In right-angled ∆OBC,
cos 60° = `("BC")/("OB")`
⇒ `1/2 = ("BC")/("OB")`
⇒ OB = 2 BC
Also, BC = BD ...[Tangent drawn from external point to circle are equal]
OB = BC + BC
⇒ OB = BC + BD
APPEARS IN
संबंधित प्रश्न
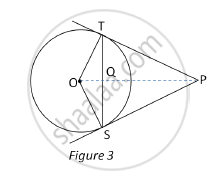
In Fig.3, from an external point P, two tangents PT and PS are drawn to a circle with centre O and radius r. If OP = 2r, show that ∠ OTS = ∠ OST = 30°.
From an external point P, tangents PA and PB are drawn to a circle with centre O. If ∠PAB = 50°, then find ∠AOB.
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
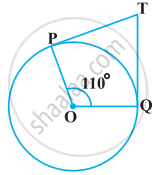
In the given figure, if TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to ______.
In the given figure, ▢ABCD is a parallelogram. It circumscribes the circle with centre T. Point E, F, G, H are touching points. If AE = 4.5, EB = 5.5, find AD.

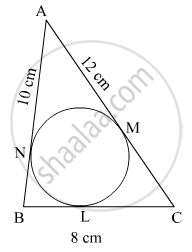
In Fig. 4, a circle is inscribed in a ΔABC having sides BC = 8 cm, AB = 10 cm and AC = 12 cm. Find the lengths BL, CM and AN.
Two concentric circles of radii a and b (a > b) are given. Find the length of the chord of the larger circle which touches the smaller circle.
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the center O at a point Q such that OQ = 13 cm. Length PQ is ______
The angle between two tangents to a circle may be 0°.
In the given figure, PA and PB are tangents from external point P to a circle with centre C and Q is any point on the circle. Then the measure of ∠AQB is ______.

