Advertisements
Advertisements
प्रश्न
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Prove that tangents drawn at the ends of a diameter of a circle are parallel to each other.
उत्तर १
Given:
CD and EF are the tangents at the end points A and B of the diameter AB of a circle with centre O.

To prove: CD || EF.
Proof: CD is the tangent to the circle at the point A.
∴ ∠BAD = 90°
EF is the tangent to the circle at the point B.
∴ ∠ABE = 90°
Thus, ∠BAD = ∠ABE (each equal to 90°).
But these are alternate interior angles.
∴ CD || EF
उत्तर २
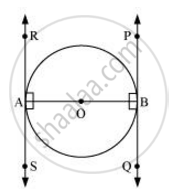
Let us assume a circle with centre O.
Let AB be the diameter of this circle.
Let RS and PQ be the tangents drawn at the two ends of the diameter AB of the circle.
So, we have to prove that RS and PQ are parallel.
Since RS is a tangent to the circle at point A and OA is the radius of the same circle.
∴ OA ⊥ RS
∴ ∠ OAR = 90°
And, ∠ OAS = 90°
Similarly, OB is the other radius of the same circle and PQ is the tangent to the circle at point B.
Hence, OB ⊥ PQ
and ∠ OBP = OBQ = 90°
Now, ∠ OAR = ∠ OBQ = 90° [Pairs of alternate interior angles.]
and ∠ OAS = ∠ OBP = 90° [Pairs of alternate interior angles.]
Since alternate interior angles RS and PQ are equal.
Hence, RS is parallel to PQ
Hence, tangents drawn at the ends of a diameter of a circle are parallel.
APPEARS IN
संबंधित प्रश्न
In the following figure, Q is the centre of a circle and PM, PN are tangent segments to the circle. If ∠MPN = 50°, find ∠MQN.

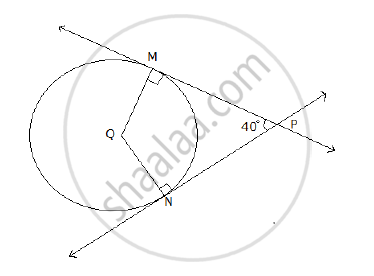
In the following figure, Q is the center of the circle. PM and PN are tangents to the circle. If ∠MPN = 40° , find ∠MQN.
Prove that the lengths of the tangents drawn from an external point to a circle are equal.
If from an external point P of a circle with centre O, two tangents PQ and PR are drawn such that ∠QPR = 120°, prove that 2PQ = PO.
In the given figure, XY and X’Y’ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X’Y’ at B. Prove that ∠AOB = 90°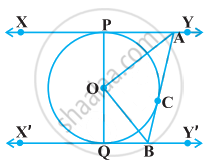
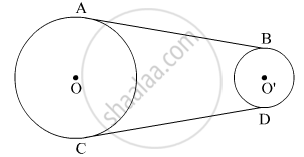
In the figure, AB and CD are common tangents to two circles of unequal radii. Prove that AB = CD.
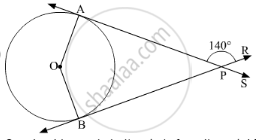
Find the angle between two radii at the centre of the circle as shown in the figure. Lines PA and PB are tangents to the circle at other ends of the radii and ∠APR = 140°.
PQ is a tangent drawn from an external point P to a circle with centre O, QOR is the diameter of the circle. If ∠POR = 120°, what is the measure of ∠OPQ?
Find the area of the shaded region in Fig. 8, where \\

M and N are the midpoints of chords AB and CD . The line MN passes through the centre O . Prove that AB || CD.
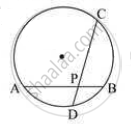
In the given figure PA = 6, PB = 4 and PC = 8. Find PD
A tangent is drawn from a point at a distance of 17 cm of circle C(0, r) of radius 8 cm. The length of its tangent is ______
The length of tangents drawn from an external point to the circle ______
The number of tangents drawn at a point of the circle is/are ______
The length of a tangent drawn from a point at a distance of 10 cm of the circle is 8 cm. The radius of the circle is ______
In the given figure, CP and CQ are tangents to a circle with centre O. ARB is another tangent touching the circle at R. If CP = 11 cm and BC = 6 cm then the length of BR is ______

The length of the tangent from an external point P on a circle with centre O is ______
The length of the tangent from an external point on a circle is ______
In a circle of radius 5 cm, AB and AC are the two chords such that AB = AC = 6 cm. Find the length of the chord BC.
PA and PB are the two tangents drawn to the circle. O is the centre of the circle. A and B are the points of contact of the tangents PA and PB with the circle. If ∠OPA = 35°, then ∠POB = ______
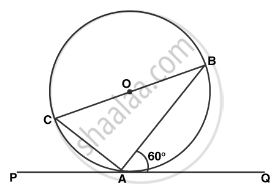
In the given figure, PAQ is the tangent. BC is the diameter of the circle. ∠BAQ = 60°, find ∠ABC.
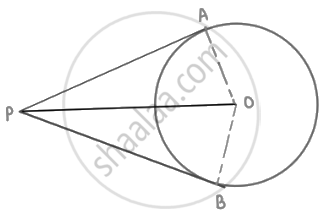
Two tangents PQ and PR are drawn from an external point to a circle with centre O. Prove that QORP is a cyclic quadrilateral.
From an external point P, two tangents, PA and PB are drawn to a circle with centre O. At one point E on the circle tangent is drawn which intersects PA and PB at C and D, respectively. If PA = 10 cm, find the the perimeter of the triangle PCD.
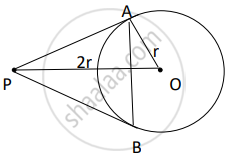
From a point P, two tangents PA and PB are drawn to a circle C(0, r). If OP = 2r, then find ∠APB. What type of triangle is APB?
In the given figure, O is the centre of circle. Find ∠AQB, given that PA and PB are tangents to the circle and ∠APB = 75°.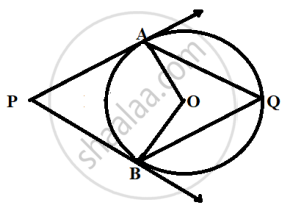
Draw two concentric circles of radii 2 cm and 3 cm. From a point on the outer circle, construct a pair of tangents to the inner circle.
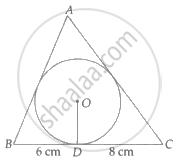
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 6 cm and 8 cm respectively. If the area of ΔABC is 84 cm2, find the lengths of sides AB and AC.
Draw two concentric circles of radii 2 cm and 5 cm. From a point P on outer circle, construct a pair of tangents to the inner circle.
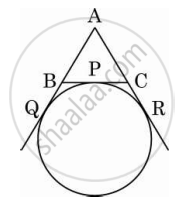
If a circle is touching the side BC of ΔABC at P and is touching AB and AC produced at Q and R respectively (see the figure). Prove that AQ = `1/2` (perimeter of ΔABC).
Two concentric circles with centre O are of radii 3 cm and 5 cm. Find the length of chord AB of the larger circle which touches the smaller circle at P.

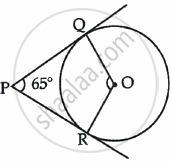
In the given figure, PQ and PR are tangents drawn from P to the circle with centre O such that ∠QPR = 65°. The measure of ∠QOR is ______.
From a point P, the length of the tangent to a circle is 24 cm and the distance of P from the centre of the circle is 25 cm. Find the radius of the circle.
In the given diagram, O is the centre of the circle. PR and PT are two tangents drawn from the external point P and touching the circle at Q and S respectively. MN is a diameter of the circle. Given ∠PQM = 42° and ∠PSM = 25°.
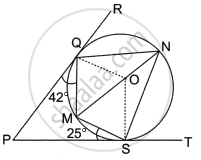
Find:
- ∠OQM
- ∠QNS
- ∠QOS
- ∠QMS
