Advertisements
Advertisements
Question
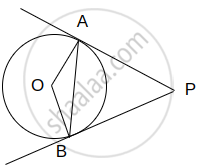
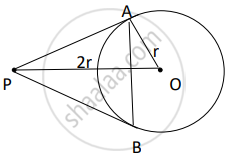
From a point P, two tangents PA and PB are drawn to a circle C(0, r). If OP = 2r, then find ∠APB. What type of triangle is APB?
Solution

Let ∠APO = θ
Sinθ = `(OA)/(OP) = 1/2` ⇒ θ = 30°
⇒ ∠APB = 2θ = 60°
Also ∠PAB = ∠PBA = 60° ......(∵ PA = PB)
⇒ ΔAPB is equilateral
APPEARS IN
RELATED QUESTIONS
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is ______.
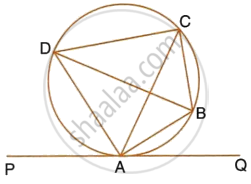
In the given figure, PQ is a tangent to the circle at A. AB and AD are bisectors of ∠CAQ and ∠PAC. If ∠BAQ = 30°, prove that : BD is diameter of the circle.
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.

Find: ∠AOB
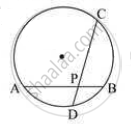
In the given figure PA = 6, PB = 4 and PC = 8. Find PD
Two concentric circles of radii a and b (a > b) are given. Find the length of the chord of the larger circle which touches the smaller circle.
The angle between two tangents to a circle may be 0°.
The length of tangent from an external point P on a circle with centre O is always less than OP.
In the given figure, there are two concentric circles with centre O. If ARC and AQB are tangents to the smaller circle from the point A lying on the larger circle, find the length of AC, if AQ = 5 cm.

PA and PB are tangents drawn to a circle of centre O from an external point P. Chord AB makes an angle of 30° with the radius at the point of contact. If length of the chord is 6 cm, find the length of the tangent PA and the length of the radius OA.