Advertisements
Advertisements
Question
The length of tangent from an external point P on a circle with centre O is always less than OP.
Options
True
False
Solution
This statement is True.
Explanation:
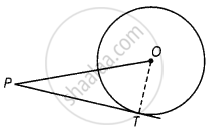
PT is a tangent drawn from external point P.
Join OT.
∵ OT ⊥ PT
So, OPT is a right-angled triangle formed.
In right-angled triangle, hypotenuse is always greater than any two of the two sides of the triangle.
∴ OP > PT
or PT < OP
APPEARS IN
RELATED QUESTIONS
In the given figure, XY and X’Y’ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X’Y’ at B. Prove that ∠AOB = 90°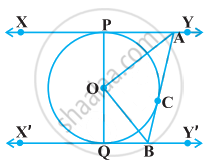
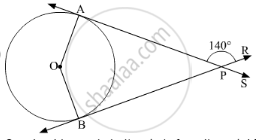
Find the angle between two radii at the centre of the circle as shown in the figure. Lines PA and PB are tangents to the circle at other ends of the radii and ∠APR = 140°.
In the given circle with center o, ∠ABC=100°, ∠ACD=40° and CT is tangent to the circle at C. find ∠ADC and ∠DCT.

M and N are the midpoints of chords AB and CD . The line MN passes through the centre O . Prove that AB || CD.
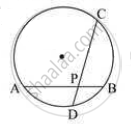
In the given figure PA = 6, PB = 4 and PC = 8. Find PD
In the given figure, ▢ABCD is a parallelogram. It circumscribes the circle with centre T. Point E, F, G, H are touching points. If AE = 4.5, EB = 5.5, find AD.

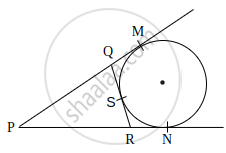
In the given figure, if a circle touches the side QR of ΔPQR at S and extended sides PQ and PR at M and N, respectively, then prove that PM = `1/2` (PQ + QR + PR)
In the given figure, BC is tangent to the circle at point B of circle centred at O. BD is a chord of the circle so that ∠BAD = 55°. Find m∠DBC.

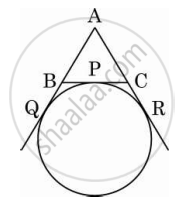
If a circle is touching the side BC of ΔABC at P and is touching AB and AC produced at Q and R respectively (see the figure). Prove that AQ = `1/2` (perimeter of ΔABC).
PA and PB are tangents drawn to a circle of centre O from an external point P. Chord AB makes an angle of 30° with the radius at the point of contact. If length of the chord is 6 cm, find the length of the tangent PA and the length of the radius OA.