Advertisements
Advertisements
Question
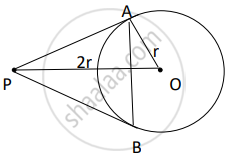
PA and PB are tangents drawn to the circle with centre O as shown in the figure. Prove that ∠APB = 2∠OAB.

Solution
Let ∠APB = x
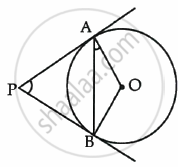
Now by theorem, the lengths of a tangents drawn from an external point to a circle are equal
So, PAB is an isosceles triangie
Therefore, ∠PAB = ∠PBA
= `1/2(180^circ - x)`
= `90^circ - x/2`
Also by theorem, the tangents at any point of a circle is perpendicular to the radius through the point of contact ∠OPT = 90°
Therefore, ∠OAB = ∠OAP – ∠PAB
= `90^circ - (90^circ - x/2)`
= `x/2`
= `1/2` ∠APB
Hence, ∠APB = 2∠OAB.
APPEARS IN
RELATED QUESTIONS
Prove that “The lengths of the two tangent segments to a circle drawn from an external point are equal.”
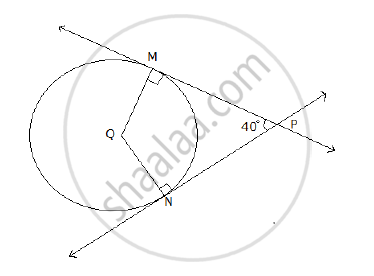
In the following figure, Q is the center of the circle. PM and PN are tangents to the circle. If ∠MPN = 40° , find ∠MQN.
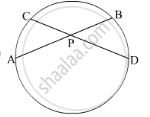
In the given figure PA = 10, PB = 2 and PC = 5. Find PD.
Two concentric circles are of radii 5 cm and 3 cm. Length of the chord of the larger circle, (in cm), which touches the smaller circle is
(A) 4
(B) 5
(C) 8
(D) 10
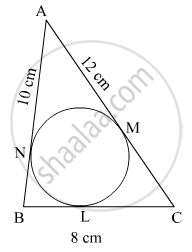
In Fig. 4, a circle is inscribed in a ΔABC having sides BC = 8 cm, AB = 10 cm and AC = 12 cm. Find the lengths BL, CM and AN.
Construct a pair of tangents to a circle of radius 4 cm from a point which is at a distance of 6 cm from its centre.
The length of tangents drawn from an external point to the circle ______
From a point P, two tangents PA and PB are drawn to a circle C(0, r). If OP = 2r, then find ∠APB. What type of triangle is APB?
In the given figure, perimeter of ΔPQR is 20 cm. Find the length of tangent PA.

Draw two concentric circles of radii 2 cm and 5 cm. From a point P on outer circle, construct a pair of tangents to the inner circle.
