Advertisements
Advertisements
प्रश्न
PA and PB are tangents drawn to the circle with centre O as shown in the figure. Prove that ∠APB = 2∠OAB.

उत्तर
Let ∠APB = x
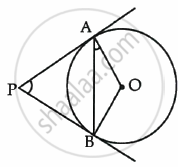
Now by theorem, the lengths of a tangents drawn from an external point to a circle are equal
So, PAB is an isosceles triangie
Therefore, ∠PAB = ∠PBA
= `1/2(180^circ - x)`
= `90^circ - x/2`
Also by theorem, the tangents at any point of a circle is perpendicular to the radius through the point of contact ∠OPT = 90°
Therefore, ∠OAB = ∠OAP – ∠PAB
= `90^circ - (90^circ - x/2)`
= `x/2`
= `1/2` ∠APB
Hence, ∠APB = 2∠OAB.
APPEARS IN
संबंधित प्रश्न
Prove that the lengths of the tangents drawn from an external point to a circle are equal.
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
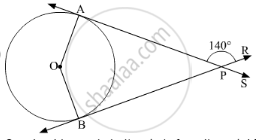
Find the angle between two radii at the centre of the circle as shown in the figure. Lines PA and PB are tangents to the circle at other ends of the radii and ∠APR = 140°.
In the given circle with center o, ∠ABC=100°, ∠ACD=40° and CT is tangent to the circle at C. find ∠ADC and ∠DCT.

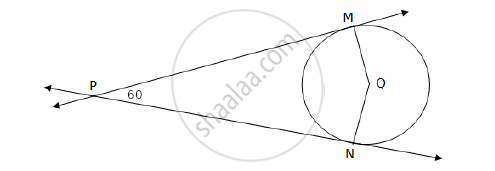
In the following figure, Q is the centre of a circle and PM, PN are tangent segments to the circle. If ∠MPN = 60°, find ∠MQN.
In a circle of radius 5 cm, AB and AC are the two chords such that AB = AC = 6 cm. Find the length of the chord BC.
In the given figure, PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q meet at a point T. Find the length of TP.

In the given figure, there are two concentric circles with centre O. If ARC and AQB are tangents to the smaller circle from the point A lying on the larger circle, find the length of AC, if AQ = 5 cm.

In the given figure, if a circle touches the side QR of ΔPQR at S and extended sides PQ and PR at M and N, respectively, then prove that PM = `1/2` (PQ + QR + PR)