Advertisements
Advertisements
प्रश्न
In the given figure, XY and X’Y’ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X’Y’ at B. Prove that ∠AOB = 90°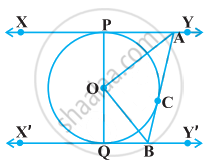
उत्तर १
Let us join point O to C.
In ΔOPA and ΔOCA,
OP = OC ...(Radii of the same circle)
AP = AC ......(Tangents from point A)
AO = AO ....(Common side)
ΔOPA ≅ ΔOCA (SSS congruence criterion)
Therefore, P ↔ C, A ↔ A, and O ↔ O
∠POA = ∠COA … (i)
Similarly, ΔOQB ≅ ΔOCB
∠QOB = ∠COB … (ii)
Since POQ is the diameter of the circle, it is a straight line.
Therefore, ∠POA + ∠COA + ∠COB + ∠QOB = 180º
From equations (i) and (ii), it can be observed that
2∠COA + 2 ∠COB = 180º
∠COA + ∠COB = 90º
∠AOB = 90°
उत्तर २
Given: XY and X'Y' are two parallel tangents to the circle with centre O touching the circle at P and Q, respectively. AB is a tangent at the point C, which intersects XY at A and X'Y' at B.
To prove: ∠AOB = 90°
Construction: Join OC.
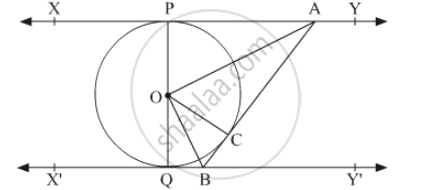
In ΔOAP and ΔOAC,
OP = OC ... (Radii of the same circle)
AP = AC. ...(Length of tangents drawn from an external point to a circle are equal)
AO = OA ....(Common side)
ΔOAP ≅ ΔOAC .....(SSS congruence criterion)
∴ ∠AOP = ∠COA ....(C.P.C.T) .....(1)
Similarly, ΔOBQ ≅ ΔOBC
∴ ∠BOQ = ∠COB .....(2)
POQ is a diameter of the circle. Hence, it is a straight line.
∴ ∠AOP + ∠COA + ∠BOQ + ∠COB = 180º
2∠COA + 2∠COB = 180º ... [From (1) and (2)]
⇒ ∠COA + ∠COB = 90º
⇒ ∠AOB = 90°
Hence proved.
APPEARS IN
संबंधित प्रश्न
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
From an external point P, tangents PA and PB are drawn to a circle with centre O. If ∠PAB = 50°, then find ∠AOB.
Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
In the given figure PA = 10, PB = 2 and PC = 5. Find PD.
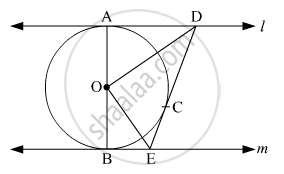
In fig. 6, l and m are two parallel tangents to a circle with centre O, touching the circle at A and B respectively. Another tangent at C intersects the line l at D and m at E. Prove that ∠DOE = 90° ?
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.
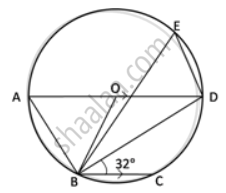
Find: ∠BED
In the given figure PA = 6, PB = 4 and PC = 8. Find PD
The number of tangents drawn at a point of the circle is/are ______
The length of a tangent drawn from a point at a distance of 10 cm of the circle is 8 cm. The radius of the circle is ______
In a circle of radius 5 cm, AB and AC are the two chords such that AB = AC = 6 cm. Find the length of the chord BC.
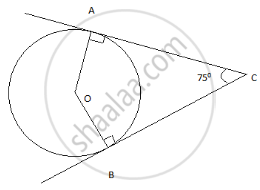
In fig, O is the centre of the circle, CA is tangent at A and CB is tangent at B drawn to the circle. If ∠ACB = 75°, then ∠AOB = ______
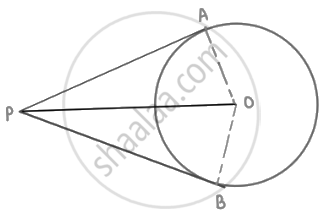
PA and PB are the two tangents drawn to the circle. O is the centre of the circle. A and B are the points of contact of the tangents PA and PB with the circle. If ∠OPA = 35°, then ∠POB = ______
In the given figure, O is the centre of circle. Find ∠AQB, given that PA and PB are tangents to the circle and ∠APB = 75°.
In the given figure, there are two concentric circles with centre O. If ARC and AQB are tangents to the smaller circle from the point A lying on the larger circle, find the length of AC, if AQ = 5 cm.

In the given figure, BC is tangent to the circle at point B of circle centred at O. BD is a chord of the circle so that ∠BAD = 55°. Find m∠DBC.

In the given figure, PA and PB are tangents from external point P to a circle with centre C and Q is any point on the circle. Then the measure of ∠AQB is ______.

From an external point, two tangents are drawn to a circle. Prove that the line joining the external point to the centre of the circle bisects the angle between the two tangents.
