Advertisements
Advertisements
Question
In Figure 1, a quadrilateral ABCD is drawn to circumscribe a circle such that its sides AB, BC, CD and AD touch the circle at P, Q, R and S respectively. If AB = x cm, BC = 7 cm, CR = 3 cm and AS = 5 cm, find x.

(A) 10
(B) 9
(C) 8
(D) 7
Solution
Given:
BC = 7 cm
CR = 3 cm
AS = 5 cm
AB = x cm
Now, BQ = BP (The lengths of the tangents drawn from an external point to a circle are equal.)
AP = AS = 5 cm ...(1)
Similarly, we have:
CR = CQ = 3 cm
BQ = BC \[-\] CQ and BC = 7 cm (Given)
⇒ BQ = BP = 4 cm ...(2)
AB = AP + PB = (5 + 4) cm = 9 cm
⇒ x = 9 cm
Hence, the correct option is B.
APPEARS IN
RELATED QUESTIONS
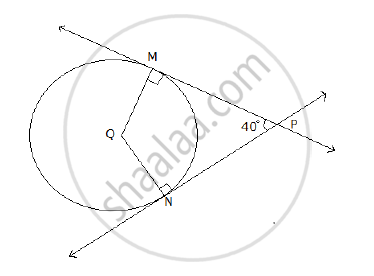
In the following figure, Q is the center of the circle. PM and PN are tangents to the circle. If ∠MPN = 40° , find ∠MQN.
Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
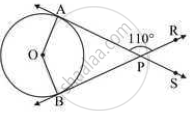
Find the angle between two radii at the centre of the circle as shown in the figure. Lines PA and PB are tangents to the circle at other ends of the radii and ∠APR = 110°.
In the given figure, ▢ABCD is a parallelogram. It circumscribes the circle with centre T. Point E, F, G, H are touching points. If AE = 4.5, EB = 5.5, find AD.

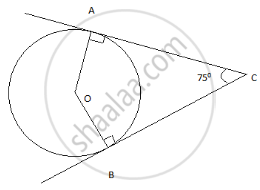
In fig, O is the centre of the circle, CA is tangent at A and CB is tangent at B drawn to the circle. If ∠ACB = 75°, then ∠AOB = ______
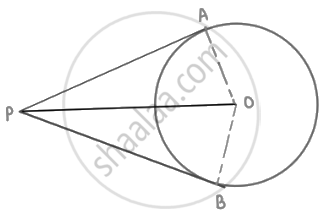
PA and PB are the two tangents drawn to the circle. O is the centre of the circle. A and B are the points of contact of the tangents PA and PB with the circle. If ∠OPA = 35°, then ∠POB = ______
The angle between two tangents to a circle may be 0°.
In the given figure, there are two concentric circles with centre O. If ARC and AQB are tangents to the smaller circle from the point A lying on the larger circle, find the length of AC, if AQ = 5 cm.

In the given figure, if a circle touches the side QR of ΔPQR at S and extended sides PQ and PR at M and N, respectively, then prove that PM = `1/2` (PQ + QR + PR)
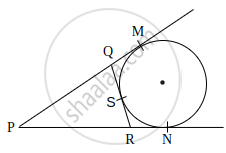
Draw two concentric circles of radii 2 cm and 5 cm. From a point P on outer circle, construct a pair of tangents to the inner circle.
