Advertisements
Advertisements
Question
3 cubes each of 8 cm edge are joined end to end. Find the total surface area of the cuboid.
Solution
The dimensions of the cuboid so formed are:
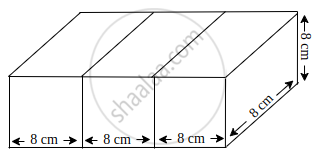
Length, l = 24 cm
Breadth, b = 8 cm
Height, h = 8 cm
Since, surface area of cuboid = 2(lb + bh + lh)
= 2(24 × 8 + 8 × 8 + 24 × 8)
= 2(192 + 64 + 192)
= 2 × 448
= 896 sq cm.
RELATED QUESTIONS
If the total surface area of a solid hemisphere is 462 cm2 , find its volume.[Take π=22/7]
From a solid cylinder of height 2.8 cm and diameter 4.2 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid [take π=22/7]
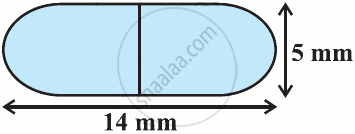
A medicine capsule is in the shape of cylinder with two hemispheres stuck to each of its ends (see the given figure). The length of the entire capsule is 14 mm and the diameter of the capsule is 5 mm. Find its surface area. [Use π = `22/7`]
In Figure 4, from a rectangular region ABCD with AB = 20 cm, a right triangle AED with AE = 9 cm and DE = 12 cm, is cut off. On the other end, taking BC as diameter, a semicircle is added on outside the region. Find the area of the shaded region.\[[Use\pi = 3 . 14]\]

A solid metallic sphere of diameter 28 cm is melted and recast into a number of smaller cones, each of diameter 4 \[\frac{2}{3}\] cm and height 3 cm. Find the number of cones so formed.
A solid metal sphere of 6 cm diameter is melted and a circular sheet of thickness 1 cm is prepared. Determine the diameter of the sheet.
A solid sphere of radius r is melted and cast into the shape of a solid cone of height r, the radius of the base of the cone is
A toy is in the form of a cylinder with hemispherical ends. If the whole length of the toy is 90 cm and its diameter is 42 cm, then find the cost of painting the toy at the rate of 70 paise per sq cm.
The shape of a gilli, in the gilli-danda game (see figure), is a combination of ______.
A solid cone of radius r and height h is placed over a solid cylinder having same base radius and height as that of a cone. The total surface area of the combined solid is `pir [sqrt(r^2 + h^2) + 3r + 2h]`.
