Advertisements
Advertisements
प्रश्न
If angle between two tangents drawn from a point P to a circle of radius a and centre O is 90°, then OP = `asqrt(2)`.
विकल्प
True
False
उत्तर
This statement is True.
Explanation:
Tangent is always perpendicular to the radius at the point of contact.
Hence, ∠RPT = 90°
If 2 tangents are drawn from an external point, then they are equally inclined to the line segment joining the centre to that point.
Consider the following figure,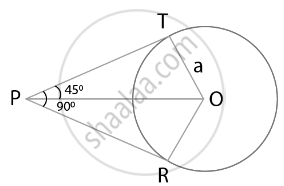
From point P, two tangents are drawn.
It is given that, OT = a
And line OP bisects ∠RPT.
So,
∠TPO = ∠RPO = 45°
We know that, OT ⊥ PT
In right-angled triangle OTP,
sin 45° = `"OT"/"OP"`
= `1/sqrt(2) = "a"/"OP"`
Hence, OP = `asqrt(2)`
APPEARS IN
संबंधित प्रश्न
In the following figure, Q is the centre of a circle and PM, PN are tangent segments to the circle. If ∠MPN = 50°, find ∠MQN.

In the below given figure, two tangents RQ and RP are drawn from an external point R to the circle with centre O. If∠PRQ = 120°, then prove that OR = PR + RQ.

Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
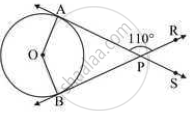
Find the angle between two radii at the centre of the circle as shown in the figure. Lines PA and PB are tangents to the circle at other ends of the radii and ∠APR = 110°.
The length of tangents drawn from an external point to the circle ______
Two concentric circles of radii a and b (a > b) are given. Find the length of the chord of the larger circle which touches the smaller circle.
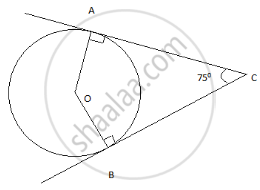
In fig, O is the centre of the circle, CA is tangent at A and CB is tangent at B drawn to the circle. If ∠ACB = 75°, then ∠AOB = ______
PA and PB are the two tangents drawn to the circle. O is the centre of the circle. A and B are the points of contact of the tangents PA and PB with the circle. If ∠OPA = 35°, then ∠POB = ______
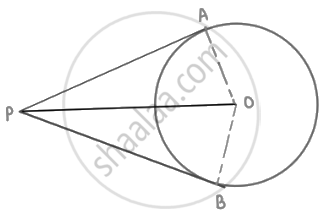
From an external point, two tangents are drawn to a circle. Prove that the line joining the external point to the centre of the circle bisects the angle between the two tangents.
