Advertisements
Advertisements
Question
In an acute-angled triangle, express a median in terms of its sides.
Solution

We have,
In ΔABC, AD is a median.
Draw AE ⊥ BC
In ΔAEB, by pythagoras theorem
AB2 = AE2 + BE2
⇒ AB2 = AD2 − DE2 + (BD − DE)2 [By Pythagoras theorem]
⇒ AB2 = AD2 − DE2 + BD2 + DE2 − 2BD × DE
⇒ AB2 = AD2 + BD2 − 2BD × DE
⇒ AB2 = AD2 + `"BC"^2/4` - BC x DE ...(i) [BC = 2BD given]
Again, In ΔAEC, by pythagoras theorem
AC2 = AE2 + EC2
⇒ AC2 = AD2 − DE2 + (DE + CD)2 [By Pythagoras theorem]
⇒AC2 = AD2 + CD2 + 2CD × DE
⇒ AC2 = AD2 + `"BC"^2/4` + BC x DE ...(ii) [BC = 2CD given]
Add equations (i) and (ii)
AB2 + AC2 = 2AD2 + `"BC"^2/2`
⇒ 2AB2 + 2AC2 = 4AD2 + BC2 [Multiply by 2]
⇒4AD2 = 2AB2 + 2AC2 − BC2
⇒ AD2 = `(2"AB"^2+2"AC"^2-"BC"^2)/4`
APPEARS IN
RELATED QUESTIONS
The sides of triangle is given below. Determine it is right triangle or not.
a = 1.6 cm, b = 3.8 cm and c = 4 cm
The lengths of the diagonals of a rhombus are 24 cm and 10 cm. Find each side of the rhombus.
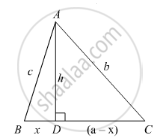
In the given figure, ∠B < 90° and segment AD ⊥ BC, show that
(i) b2 = h2 + a2 + x2 - 2ax
(ii) b2 = a2 + c2 - 2ax
∆ABD is a right triangle right-angled at A and AC ⊥ BD. Show that
(i) AB2 = BC x BD
(ii) AC2 = BC x DC
(iii) AD2 = BD x CD
(iv) `"AB"^2/"AC"^2="BD"/"DC"`
Determine whether the triangle having sides (a − 1) cm, 2`sqrta` cm and (a + 1) cm is a right-angled
triangle.
State Pythagoras theorem
If D, E, F are the respectively the midpoints of sides BC, CA and AB of ΔABC. Find the ratio of the areas of ΔDEF and ΔABC.
Find the length of each side of a rhombus whose diagonals are 24cm and 10cm long.
Find the diagonal of a rectangle whose length is 16 cm and area is 192 sq.cm ?
A girl walks 200m towards East and then 150m towards North. The distance of the girl from the starting point is ______.
