Advertisements
Advertisements
Question
Determine whether the triangle having sides (a − 1) cm, 2`sqrta` cm and (a + 1) cm is a right-angled
triangle.
Solution
Let ABC be the Δ with
AB = (a – 1) cm BC = 2`sqrta` cm, CA = (a + 1) cm
Hence, AB2 = (a − 1)2 = a2 + 1 − 2𝑎
BC2 = (2`sqrta`)2 = 4a
CA2 = (a + 1)2 = a2 + 1 + 2a
Hence AB2 + BC2 = AC2
So Δ ABC is right angled Δ at B.
APPEARS IN
RELATED QUESTIONS
Using Pythagoras theorem determine the length of AD in terms of b and c shown in Figure.
ABCD is a square. F is the mid-point of AB. BE is one third of BC. If the area of ΔFBE = 108 cm2, find the length of AC.
The lengths of the diagonals of a rhombus are 24 cm and 10 cm. Find each side of the rhombus.
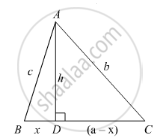
In Figure, D is the mid-point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED
= x, AD = p and AE = h, prove that:
(i) `b^2 = p^2 + ax + a^2/4`
(ii) `c^2 = p^2 - ax + a^2/4`
(iii) `b^2 + c^2 = 2p^2 + a^2/2`
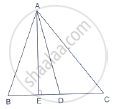
In the given figure, ∠B < 90° and segment AD ⊥ BC, show that
(i) b2 = h2 + a2 + x2 - 2ax
(ii) b2 = a2 + c2 - 2ax
In a quadrilateral ABCD, ∠B = 90°, AD2 = AB2 + BC2 + CD2, prove that ∠ACD = 90°.
A man goes 12m due south and then 35m due west. How far is he from the starting point.
Find the length of each side of a rhombus are 40 cm and 42 cm. find the length of each side of the rhombus.
A girl walks 200m towards East and then 150m towards North. The distance of the girl from the starting point is ______.
In a ΔABC, ∠CAB is an obtuse angle. P is the circumcentre of ∆ABC. Prove that ∠CAB – ∠PBC = 90°.
