Advertisements
Advertisements
Question
In a ΔABC, ∠CAB is an obtuse angle. P is the circumcentre of ∆ABC. Prove that ∠CAB – ∠PBC = 90°.
Solution
Given: ∠CAB is an obtuse angle and P is the circumcentre of ΔABC.
Construction: Draw BD as diameter, join AD.
Proof: ∠CAD = ∠CBD ......[Angles on same arc]
⇒ ∠CAD = ∠CBP ......(i)
Also, ∠BAD = 90° ......(ii) [Angle in semi-circle]
Now, from figure,
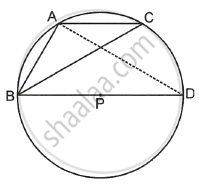
∠CAB = ∠CAD + ∠DAB
⇒ ∠CAB = ∠CBP + 90° ......[Using (i) and (ii)]
⇒ ∠CAB – ∠CBP = 90°
or ∠CAB – ∠PBC = 90°.
Hence proved.
APPEARS IN
RELATED QUESTIONS
If the sides of a triangle are 3 cm, 4 cm, and 6 cm long, determine whether the triangle is a right-angled triangle.
The sides of triangle is given below. Determine it is right triangle or not.
a = 9 cm, b = l6 cm and c = 18 cm
The sides of triangle is given below. Determine it is right triangle or not.
a = 1.6 cm, b = 3.8 cm and c = 4 cm
A ladder 17 m long reaches a window of a building 15 m above the ground. Find the distance of the foot of the ladder from the building.
In an isosceles triangle ABC, AB = AC = 25 cm, BC = 14 cm. Calculate the altitude from A on BC.
Two poles of height 9 m and 14 m stand on a plane ground. If the distance between their feet is 12 m, find the distance between their tops.
A triangle has sides 5 cm, 12 cm and 13 cm. Find the length to one decimal place, of the perpendicular from the opposite vertex to the side whose length is 13 cm.
Calculate the height of an equilateral triangle each of whose sides measures 12 cm.
In right-angled triangle ABC in which ∠C = 90°, if D is the mid-point of BC, prove that AB2 = 4AD2 − 3AC2.
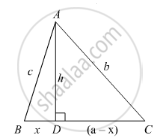
In the given figure, ∠B < 90° and segment AD ⊥ BC, show that
(i) b2 = h2 + a2 + x2 - 2ax
(ii) b2 = a2 + c2 - 2ax
In ∆ABC, ∠A is obtuse, PB ⊥ AC and QC ⊥ AB. Prove that:
(i) AB ✕ AQ = AC ✕ AP
(ii) BC2 = (AC ✕ CP + AB ✕ BQ)
In a right ∆ABC right-angled at C, if D is the mid-point of BC, prove that BC2 = 4(AD2 − AC2).
In an equilateral ΔABC, AD ⊥ BC, prove that AD2 = 3BD2.
∆ABD is a right triangle right-angled at A and AC ⊥ BD. Show that
(i) AB2 = BC x BD
(ii) AC2 = BC x DC
(iii) AD2 = BD x CD
(iv) `"AB"^2/"AC"^2="BD"/"DC"`
Find the length of the altitude of an equilateral triangle of side 2a cm.
Find the length of each side of a rhombus are 40 cm and 42 cm. find the length of each side of the rhombus.
From given figure, In ∆ABC, AB ⊥ BC, AB = BC, AC = `5sqrt(2)` , then what is the height of ∆ABC?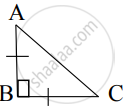
A girl walks 200m towards East and then 150m towards North. The distance of the girl from the starting point is ______.
Find the altitude of an equilateral triangle of side 8 cm.
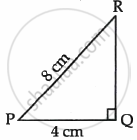
In the given figure, ΔPQR is a right triangle right angled at Q. If PQ = 4 cm and PR = 8 cm, then P is ______.