Advertisements
Advertisements
प्रश्न
An aeroplane leaves an airport and flies due north at a speed of 1000km/hr. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km/hr. How far apart will be the two planes after 1 hours?
उत्तर
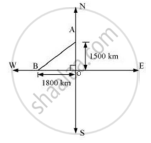
Distance traveled by the plane flying towards north in `1 1/2`hrs
`= 1000xx1 1/2=1500`km
Similarly, distance travelled by the plane flying towards west in `1 1/2`hrs
`=1200xx1 1/2=1800`km
Let these distances are represented by OA and OB respectively.
Now applying Pythagoras theorem
Distance between these planes after `1 1/2`hrs AB `=sqrt(OA^2+OB^2)`
`=sqrt(1500^2+1800^2)`
`=sqrt(2250000+3240000)`
`=sqrt5490000`
`=sqrt(9xx610000)`
`=300sqrt61`
So, distance between these planes will be `300sqrt61` km, after `1 1/2`hrs
APPEARS IN
संबंधित प्रश्न
If the sides of a triangle are 3 cm, 4 cm, and 6 cm long, determine whether the triangle is a right-angled triangle.
A triangle has sides 5 cm, 12 cm and 13 cm. Find the length to one decimal place, of the perpendicular from the opposite vertex to the side whose length is 13 cm.
ABCD is a square. F is the mid-point of AB. BE is one third of BC. If the area of ΔFBE = 108 cm2, find the length of AC.
In an isosceles triangle ABC, if AB = AC = 13 cm and the altitude from A on BC is 5 cm, find BC.
Each side of a rhombus is 10 cm. If one of its diagonals is 16 cm find the length of the other diagonal.
Find the length of the altitude of an equilateral triangle of side 2a cm.
A man goes 12m due south and then 35m due west. How far is he from the starting point.
Find the side and perimeter of a square whose diagonal is `13sqrt2` cm.
From given figure, In ∆ABC, AB ⊥ BC, AB = BC, AC = `5sqrt(2)` , then what is the height of ∆ABC?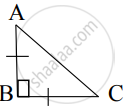
A girl walks 200m towards East and then 150m towards North. The distance of the girl from the starting point is ______.
