NCERT Exemplar solutions for Mathematics [English] Class 10 chapter 4 - Quadatric Euation [Latest edition]

Which of the following is a quadratic equation?

Which of the following is not a quadratic equation?

Which of the following equations has 2 as a root?

If `(1)/(2)` is a root of the equation `x^2 + kx - (5)/(4) = 0`, then the value of k is ______.

Which of the following equations has the sum of its roots as 3?

Values of k for which the quadratic equation 2x² – kx + k = 0 has equal roots is ______.

Which constant must be added and subtracted to solve the quadratic equation `9x^2 + 3/4x - sqrt(2) = 0` by the method of completing the square?

The quadratic equation `2x^2 - sqrt(5)x + 1 = 0` has ______.

Which of the following equations has two distinct real roots?

Which of the following equations has no real roots?

(x² + 1)² – x² = 0 has ______.

State whether the following quadratic equation have two distinct real roots. Justify your answer.

x² – 3x + 4 = 0

State whether the following quadratic equation have two distinct real roots. Justify your answer.

2x² + x – 1 = 0

State whether the following quadratic equation have two distinct real roots. Justify your answer.

`2x^2 - 6x + 9/2 = 0`

State whether the following quadratic equation have two distinct real roots. Justify your answer.

3x² – 4x + 1 = 0

State whether the following quadratic equation have two distinct real roots. Justify your answer.

(x + 4)² – 8x = 0

State whether the following quadratic equation have two distinct real roots. Justify your answer.

`(x - sqrt(2))^2 - 2(x + 1) = 0`

State whether the following quadratic equation have two distinct real roots. Justify your answer.

`sqrt(2)x^2 - 3/sqrt(2)x + 1/sqrt(2) = 0`

State whether the following quadratic equation have two distinct real roots. Justify your answer.

x(1 – x) – 2 = 0

State whether the following quadratic equation have two distinct real roots. Justify your answer.

(x – 1)(x + 2) + 2 = 0

State whether the following quadratic equation have two distinct real roots. Justify your answer.

(x + 1)(x – 2) + x = 0

Every quadratic equation has exactly one root.

Every quadratic equation has at least one real root.

Every quadratic equation has at least two roots.

Every quadratic equations has at most two roots.

If the coefficient of x² and the constant term of a quadratic equation have opposite signs, then the quadratic equation has real roots.

If the coefficient of x² and the constant term have the same sign and if the coefficient of x term is zero, then the quadratic equation has no real roots.

A quadratic equation with integral coefficient has integral roots. Justify your answer.

Does there exist a quadratic equation whose coefficients are rational but both of its roots are irrational? Justify your answer.

Does there exist a quadratic equation whose coefficients are all distinct irrationals but both the roots are rationals? Why?

Is 0.2 a root of the equation x² – 0.4 = 0? Justify

If b = 0, c < 0, is it true that the roots of x² + bx + c = 0 are numerically equal and opposite in sign? Justify.

Find the roots of the quadratic equation by using the quadratic formula in the following:

2x² – 3x – 5 = 0

Find the roots of the quadratic equation by using the quadratic formula in the following:

5x² + 13x + 8 = 0

Find the roots of the quadratic equation by using the quadratic formula in the following:

–3x² + 5x + 12 = 0

Find the roots of the quadratic equation by using the quadratic formula in the following:

–x² + 7x – 10 = 0

Find the roots of the quadratic equation by using the quadratic formula in the following:

`x^2 + 2sqrt(2)x - 6 = 0`

Find the roots of the quadratic equation by using the quadratic formula in the following:

`x^2 - 3sqrt(5)x + 10 = 0`

Find the roots of the quadratic equation by using the quadratic formula in the following:

`1/2x^2 - sqrt(11)x + 1 = 0`

Find the roots of the following quadratic equation by the factorisation method:

`2x^2 + 5/3x - 2 = 0`

Find the roots of the following quadratic equation by the factorisation method:

`2/5x^2 - x - 3/5 = 0`

Find the roots of the following quadratic equation by the factorisation method:

`3sqrt(2)x^2 - 5x - sqrt(2) = 0`

Find the roots of the following quadratic equation by the factorisation method:

`3x^2 + 5sqrt(5)x - 10 = 0`

Find the roots of the following quadratic equation by the factorisation method:

`21x^2 - 2x + 1/21 = 0`

Find whether the following equation have real roots. If real roots exist, find them.

8x² + 2x – 3 = 0

Find whether the following equation have real roots. If real roots exist, find them.

–2x² + 3x + 2 = 0

Find whether the following equation have real roots. If real roots exist, find them.

5x² – 2x – 10 = 0

Find whether the following equation have real roots. If real roots exist, find them.

`1/(2x - 3) + 1/(x - 5) = 1, x ≠ 3/2, 5`

Find whether the following equation have real roots. If real roots exist, find them.

`x^2 + 5sqrt(5)x - 70 = 0`

Find a natural number whose square diminished by 84 is equal to thrice of 8 more than the given number.

A natural number, when increased by 12, equals 160 times its reciprocal. Find the number.

A train, travelling at a uniform speed for 360 km, would have taken 48 minutes less to travel the same distance if its speed were 5 km/h more. Find the original speed of the train.

If Zeba were younger by 5 years than what she really is, then the square of her age (in years) would have been 11 more than five times her actual age. What is her age now?

At present Asha’s age (in years) is 2 more than the square of her daughter Nisha’s age. When Nisha grows to her mother’s present age, Asha’s age would be one year less than 10 times the present age of Nisha. Find the present ages of both Asha and Nisha.

In the centre of a rectangular lawn of dimensions 50 m × 40 m, a rectangular pond has to be constructed so that the area of the grass surrounding the pond would be 1184 m² [see figure]. Find the length and breadth of the pond.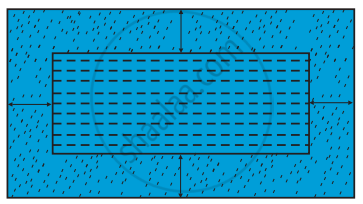

At t minutes past 2 pm, the time needed by the minutes hand of a clock to show 3 pm was found to be 3 minutes less than `t^2/4` minutes. Find t.