Advertisements
Advertisements
Question
In the centre of a rectangular lawn of dimensions 50 m × 40 m, a rectangular pond has to be constructed so that the area of the grass surrounding the pond would be 1184 m2 [see figure]. Find the length and breadth of the pond.
Solution
Given that a rectangular pond has to be constructed in the centre of a rectangular lawn of dimensions 50 m × 40 m
So, the distance between pond and lawn would be same around the pond.
Say x m.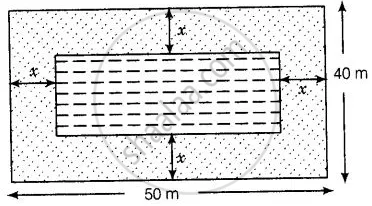
Now, length of rectangular lawn (l1) = 50 m and breadth of rectangular lawn (b1) = 40 m
Length of rectangular pond (l2)= 50 – (x + x) = 50 – 2x
And breadth of rectangular pond (b2) = 40 – (x + x)= 40 – 2x
Also, area of the grass surrounding the pond = 1184 m2
Area of rectangular lawn – Area of rectangular pond = Area of grass surrounding the pond
l1 × b1 – l2 × b2 = 1184 ......[∵ Area of rectangle = length × breadth]
⇒ 50 × 40 – (50 – 2x)(40 – 2x) = 1184
⇒ 2000 – (2000 – 80x – 100x + 4x2) = 1184
⇒ 80x + 100x – 4x2 = 1184
⇒ 4x2 – 180x + 1184 = 0
⇒ x2 – 45x + 296 = 0
⇒ x2 – 37x – 8x + 296 = 0 ....[By splitting the middle term]
⇒ x(x – 37) – 8(x – 37) = 0
⇒ (x – 37)(x – 8) = 0
∴ x = 8
At x = 37,
Length and Breadth of pond are – 24 and – 34, respectively but length and breadth cannot be negative.
So, x = 37 cannot be possible
∴ Length of pond = 50 – 2x
= 50 – 2(8)
= 50 – 16
= 34 m
And breadth of pond = 40 – 2x
= 40 – 2(8)
= 40 – 16
= 24 m
Hence, required length and breadth of pond are 34 m and 24 m, respectively.
APPEARS IN
RELATED QUESTIONS
Solve the following quadratic equations by factorization:
9x2 − 3x − 2 = 0
Solve the following quadratic equations by factorization:
5x2 - 3x - 2 = 0
The perimeter of a rectangular field is 82 m and its area is 400 m2. Find the breadth of the rectangle.
For the equation given below, find the value of ‘m’ so that the equation has equal roots. Also find the solution of the equation:
3x2 + 12x + (m + 7) = 0
Solve the following equation: 4x2 + 16x = 0
If an integer is added to its square the sum is 90. Find the integer with the help of a quadratic equation.
In each of the following determine whether the given values are solutions of the equation or not.
3x2 - 2x - 1 = 0; x = 1
Find three successive even natural numbers, the sum of whose squares is 308.
A person was given Rs. 3000 for a tour. If he extends his tour programme by 5 days, he must cut down his daily expenses by Rs. 20. Find the number of days of his tour programme.
The hypotenuse of a right-angled triangle is 1 m less than twice the shortest side. If the third side is 1 m more than the shortest side, find the sides of the triangle.
