Advertisements
Advertisements
प्रश्न
In the centre of a rectangular lawn of dimensions 50 m × 40 m, a rectangular pond has to be constructed so that the area of the grass surrounding the pond would be 1184 m2 [see figure]. Find the length and breadth of the pond.
उत्तर
Given that a rectangular pond has to be constructed in the centre of a rectangular lawn of dimensions 50 m × 40 m
So, the distance between pond and lawn would be same around the pond.
Say x m.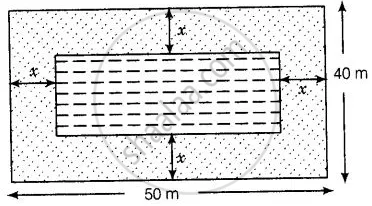
Now, length of rectangular lawn (l1) = 50 m and breadth of rectangular lawn (b1) = 40 m
Length of rectangular pond (l2)= 50 – (x + x) = 50 – 2x
And breadth of rectangular pond (b2) = 40 – (x + x)= 40 – 2x
Also, area of the grass surrounding the pond = 1184 m2
Area of rectangular lawn – Area of rectangular pond = Area of grass surrounding the pond
l1 × b1 – l2 × b2 = 1184 ......[∵ Area of rectangle = length × breadth]
⇒ 50 × 40 – (50 – 2x)(40 – 2x) = 1184
⇒ 2000 – (2000 – 80x – 100x + 4x2) = 1184
⇒ 80x + 100x – 4x2 = 1184
⇒ 4x2 – 180x + 1184 = 0
⇒ x2 – 45x + 296 = 0
⇒ x2 – 37x – 8x + 296 = 0 ....[By splitting the middle term]
⇒ x(x – 37) – 8(x – 37) = 0
⇒ (x – 37)(x – 8) = 0
∴ x = 8
At x = 37,
Length and Breadth of pond are – 24 and – 34, respectively but length and breadth cannot be negative.
So, x = 37 cannot be possible
∴ Length of pond = 50 – 2x
= 50 – 2(8)
= 50 – 16
= 34 m
And breadth of pond = 40 – 2x
= 40 – 2(8)
= 40 – 16
= 24 m
Hence, required length and breadth of pond are 34 m and 24 m, respectively.
APPEARS IN
संबंधित प्रश्न
Sum of two numbers is 16. The sum of their reciprocals is 1/3. Find the numbers.
A pole has to be erected at a point on the boundary of a circular park of diameter 13 meters in such a way that the difference of its distances from two diametrically opposite fixed gates A and B on the boundary is 7 meters. Is it the possible to do so? If yes, at what distances from the two gates should the pole be erected?
The difference of two natural numbers is 5 and the difference of heir reciprocals is `5/14`Find the numbers
Find the roots of the quadratic equation \[\sqrt{2} x^2 + 7x + 5\sqrt{2} = 0\].
If 2 is a root of the quadratic equation \[3 x^2 + px - 8 = 0\] and the quadratic equation \[4 x^2 - 2px + k = 0\] has equal roots, find the value of k.
Solve equation using factorisation method:
(x + 3)2 – 4(x + 3) – 5 = 0
Solve the following equation by factorization
`4sqrt(3)x^2 + 5x - 2sqrt(3)` = 0
Solve the following equation by factorization
`x + (1)/x = 2(1)/(20)`
An aeroplane flying with a wind of 30 km/hr takes 40 minutes less to fly 3600 km, than what it would have taken to fly against the same wind. Find the planes speed of flying in still air.
If x4 – 5x2 + 4 = 0; the values of x are ______.
